Pirámide elongada
poliedro construido uniendo una pirámide a un prisma
En geometría, las pirámides elongadas[1] son un conjunto infinito de poliedros, construidos al unir una pirámide n-gonal a un prisma n-gonal. Junto con el conjunto de pirámides, estas figuras son topológicamente autoduales.
| Pirámide elongada | ||
|---|---|---|
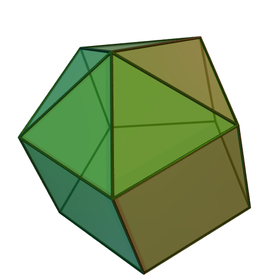 Ejemplo: forma de base pentagonal | ||
| Caras |
n triángulos n cuadrados 1 n-gono | |
| Aristas | 4n | |
| Vértices | 2n + 1 | |
| Grupo de simetría | Cnv, [n], (*nn) | |
| Grupo de rotación | Cn, [n]+, (nn) | |
| Poliedro dual | Autodual | |
| Propiedades | ||
| Convexo | ||
Hay tres pirámides elongadas que son sólidos de Johnson:
- La pirámide triangular elongada (J7),
- La pirámide cuadrada elongada (J8), y
- La pirámide pentagonal elongada (J9).
También se pueden construir formas superiores empleando pirámides formadas por triángulos isósceles sobre prismas formados por polígonos regulares de más caras.
Ejemplos
editar| Nombre | Caras | |
|---|---|---|
| Pirámide triangular elongada (J7) | 3+1 triángulos, 3 cuadrados | |
| Pirámide cuadrada elongada (J8) | 4 triángulos, 4+1 cuadrados | |
| Pirámide pentagonal elongada (J9) | 5 triángulos, 5 cuadrados, 1 pentágono |
Véase también
editarReferencias
editar- ↑ A. R. Rajwade (2001). Convex Polyhedra with Regularity Conditions and Hilbert’s Third Problem. Springer. pp. 89 de 128. ISBN 9789386279064. Consultado el 30 de octubre de 2023.
Bibliografía
editar- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, páginas 169-200. Contiene la enumeración original de los 92 sólidos y la conjetura de que no existen otros.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. La primera prueba de que solo hay 92 sólidos de Johnson.