Integral trigonométrica cardinal

En matemáticas, las funciones integrales trigonométricas cardinales son una familia de integrales no elementales que involucran funciones trigonométricas cardinales (aquellas que consisten en dividir una función trigonométrica en una variable, por la propia variable).

Gráfico de la función integral seno hiperbólico Shi(z) en el plano complejo de -2-2i a 2+2i, con colores creados con la función ComplexPlot3D de Mathematica 13.1

Si(x) (azul) y Ci(x) (verde) representadas en el mismo gráfico

Integral seno en el plano complejo, trazado con una variante de coloreado de dominios

Integral coseno en el plano complejo. Obsérvese la rama cortada a lo largo del eje real negativo

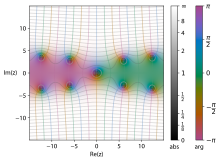
Integral senoidal

Gráfica de Si(x) para 0 ≤ x ≤ 8 π

Gráfica de la función integral coseno Ci(z) en el plano complejo de -2-2i a 2+2i con colores creados con la función ComplexPlot3D de Mathematica 13.1

Las diferentes definiciones de la integral seno son:

$\operatorname {Si} (x)=\int _{0}^{x}{\frac {\sin t}{t}}\,dt$

$\operatorname {si} (x)=-\int _{x}^{\infty }{\frac {\sin t}{t}}\,dt~.$

Téngase en cuenta que el integrando ${\frac {\sin(t)}{t}}$ es el seno cardinal, y también la función de Bessel esférica de orden cero. Dado que sinc es una función completa par (función holomorfa en todo el plano complejo), Si es entera, impar y para la integral de su definición se puede tomar cualquier recorrido que conecte los puntos extremos.

Por definición, Si(x) es la primitiva de sin x / x cuyo valor es cero en x= 0, y si(x) es la primitiva cuyo valor es cero en x= ∞. Su diferencia está dada por la integral de Dirichlet,

$\operatorname {Si} (x)-\operatorname {si} (x)=\int _{0}^{\infty }{\frac {\sin t}{t}}\,dt={\frac {\pi }{2}}\quad {\text{ o }}\quad \operatorname {Si} (x)={\frac {\pi }{2}}+\operatorname {si} (x)~.$

En procesamiento de señales, las oscilaciones de la integral sinusoidal provocan sobrepasos y artefactos de anillo cuando se usa un filtro Sinc, y el dominio de la frecuencia resuena si se usa un filtro sinc truncado como filtro de paso bajo.

La función está relacionada con el fenómeno de Gibbs: si se considera la integral seno como la convolución de la función sinc con la función escalón de Heaviside, esto corresponde a truncar la serie de Fourier, que es la causa del fenómeno de Gibbs.

Integral cosenoidal

Gráfica de Ci(x) para 0 < x ≤ 8π

Las diferentes definiciones de la integral cosenoidal son:

$\operatorname {Cin} (x)=\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt~,$

$\operatorname {Ci} (x)=-\int _{x}^{\infty }{\frac {\cos t}{t}}\,dt=\gamma +\ln x-\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt\qquad ~{\text{ para }}~\left|\operatorname {Arg} (x)\right|<\pi ~,$

donde γ ≈ 0.57721566 ... es el Constante de Euler-Mascheroni. Algunos textos utilizan ci en lugar de Ci.

Ci(x) es la primitiva de cos x / x (que se anula cuando $x\to \infty$). Las dos definiciones están relacionadas por

$\operatorname {Ci} (x)=\gamma +\ln x-\operatorname {Cin} (x)~.$

Cin es una función completa par. Por esta razón, algunos textos tratan a Cin como la función principal y deducen Ci a partir de Cin.

Integral seno hiperbólico

La integral seno hiperbólico se define como:

$\operatorname {Shi} (x)=\int _{0}^{x}{\frac {\sinh(t)}{t}}\,dt.$

Está relacionada con la integral seno ordinaria por

$\operatorname {Si} (ix)=i\operatorname {Shi} (x).$

Integral coseno hiperbólico

Gráfico de la función integral del coseno hiperbólico Chi(z) en el plano complejo de -2-2i a 2+2i, con colores creados con la función ComplexPlot3D de Mathematica 13.1

La integral coseno hiperbólico es:

$\operatorname {Chi} (x)=\gamma +\ln x+\int _{0}^{x}{\frac {\cosh t-1}{t}}\,dt\qquad ~{\text{ para }}~\left|\operatorname {Arg} (x)\right|<\pi ~,$

donde $\gamma$ es la constante de Euler-Mascheroni.

Tiene la siguiente expansión en serie:

$\operatorname {Chi} (x)=\gamma +\ln(x)+{\frac {x^{2}}{4}}+{\frac {x^{4}}{96}}+{\frac {x^{6}}{4320}}+{\frac {x^{8}}{322560}}+{\frac {x^{10}}{36288000}}+O(x^{12}).$

Funciones auxiliares

Las integrales trigonométricas se pueden entender en términos de las llamadas "funciones auxiliares":

${\begin{array}{rcl}f(x)&\equiv &\int _{0}^{\infty }{\frac {\sin(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {e^{-xt}}{t^{2}+1}}\,dt&=&\operatorname {Ci} (x)\sin(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)~,\\g(x)&\equiv &\int _{0}^{\infty }{\frac {\cos(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {te^{-xt}}{t^{2}+1}}\,dt&=&-\operatorname {Ci} (x)\cos(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)~.\end{array}}$

Usando estas funciones, las integrales trigonométricas se pueden reexpresar como: (cf. Abramowitz y Stegun, p. 232)

${\begin{array}{rcl}{\frac {\pi }{2}}-\operatorname {Si} (x)=-\operatorname {si} (x)&=&f(x)\cos(x)+g(x)\sin(x)~,\qquad {\text{ y }}\\\operatorname {Ci} (x)&=&f(x)\sin(x)-g(x)\cos(x)~.\\\end{array}}$

Espiral de Nielsen

Espiral de Nielsen

La espiral formado por el gráfico de la expresión paramétrica de si , ci se conoce como espiral de Nielsen:

$x(t)=a\times \operatorname {ci} (t)$

$y(t)=a\times \operatorname {si} (t)$

La espiral está estrechamente relacionada con las integrales de Fresnel y la clotoide. La espiral de Nielsen tiene aplicaciones en el procesamiento de la visión, la construcción de carreteras y vías y otras áreas de la ingeniería.​

Expansión

Se pueden utilizar varias expansiones para la evaluación de integrales trigonométricas, según el rango del argumento.

Serie asintótica (para argumentos amplios)

$\operatorname {Si} (x)\sim {\frac {\pi }{2}}-{\frac {\cos x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\sin x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)$

$\operatorname {Ci} (x)\sim {\frac {\sin x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\cos x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)~.$

Estas series son asintóticas y divergentes, aunque pueden usarse para estimaciones e incluso evaluaciones precisas en ℜ(x) ≫ 1.

Serie convergente

$\operatorname {Si} (x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)(2n+1)!}}=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}\pm \cdots$

$\operatorname {Ci} (x)=\gamma +\ln x+\sum _{n=1}^{\infty }{\frac {(-1)^{n}x^{2n}}{2n(2n)!}}=\gamma +\ln x-{\frac {x^{2}}{2!\cdot 2}}+{\frac {x^{4}}{4!\cdot 4}}\mp \cdots$

Estas series son convergentes en cualquier x complejo, aunque para |x| ≫ 1, la serie convergerá lentamente inicialmente, lo que requerirá muchos términos para obtener una alta precisión.

Desarrollo en serie

De la expansión de la serie de Maclaurin del seno

$\sin \,x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+{\frac {x^{9}}{9!}}-{\frac {x^{11}}{11!}}+\cdots$

se obiene:

${\frac {\sin \,x}{x}}=1-{\frac {x^{2}}{3!}}+{\frac {x^{4}}{5!}}-{\frac {x^{6}}{7!}}+{\frac {x^{8}}{9!}}-{\frac {x^{10}}{11!}}+\cdots$

y de aquí se pasa a:

$\therefore \int {\frac {\sin \,x}{x}}dx=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}+{\frac {x^{9}}{9!\cdot 9}}-{\frac {x^{11}}{11!\cdot 11}}+\cdots$

Relación con la integral exponencial del argumento imaginario

La función

$\operatorname {E} _{1}(z)=\int _{1}^{\infty }{\frac {\exp(-zt)}{t}}\,dt\qquad ~{\text{ para }}~\Re (z)\geq 0$

se llama integral exponencial. Está estrechamente relacionada con Si y Ci,

$\operatorname {E} _{1}(ix)=i\left(-{\frac {\pi }{2}}+\operatorname {Si} (x)\right)-\operatorname {Ci} (x)=i\operatorname {si} (x)-\operatorname {ci} (x)\qquad ~{\text{ para }}~x>0~.$

Como cada función respectiva es analítica, excepto el corte en valores negativos del argumento, el área de validez de la relación debe extenderse (fuera de este rango, en la expresión aparecen términos adicionales que son factores enteros de π).

Los casos de argumento imaginario de la función integroexponencial generalizada son

$\int _{1}^{\infty }\cos(ax){\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}+\sum _{n\geq 1}{\frac {(-a^{2})^{n}}{(2n)!(2n)^{2}}}~,$

que es la parte real de

$\int _{1}^{\infty }e^{iax}{\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}-{\frac {\pi }{2}}i\left(\gamma +\ln a\right)+\sum _{n\geq 1}{\frac {(ia)^{n}}{n!n^{2}}}~.$

Similarmente,

$\int _{1}^{\infty }e^{iax}{\frac {\ln x}{x^{2}}}\,dx=1+ia\left[-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a-1\right)+{\frac {\ln ^{2}a}{2}}-\ln a+1\right]+{\frac {\pi a}{2}}{\Bigl (}\gamma +\ln a-1{\Bigr )}+\sum _{n\geq 1}{\frac {(ia)^{n+1}}{(n+1)!n^{2}}}~.$

Evaluación eficiente

La aproximación de Padé de la serie de Taylor convergente proporciona una forma eficiente de evaluar funciones para argumentos pequeños. Las siguientes fórmulas, dadas por Rowe et al. (2015),​ tienen una precisión mejor que 10⁻¹⁶ para 0 ≤ x ≤ 4,

${\begin{array}{rcl}\operatorname {Si} (x)&\approx &x\cdot \left({\frac {\begin{array}{l}1-4.54393409816329991\cdot 10^{-2}\cdot x^{2}+1.15457225751016682\cdot 10^{-3}\cdot x^{4}-1.41018536821330254\cdot 10^{-5}\cdot x^{6}\\~~~+9.43280809438713025\cdot 10^{-8}\cdot x^{8}-3.53201978997168357\cdot 10^{-10}\cdot x^{10}+7.08240282274875911\cdot 10^{-13}\cdot x^{12}\\~~~-6.05338212010422477\cdot 10^{-16}\cdot x^{14}\end{array}}{\begin{array}{l}1+1.01162145739225565\cdot 10^{-2}\cdot x^{2}+4.99175116169755106\cdot 10^{-5}\cdot x^{4}+1.55654986308745614\cdot 10^{-7}\cdot x^{6}\\~~~+3.28067571055789734\cdot 10^{-10}\cdot x^{8}+4.5049097575386581\cdot 10^{-13}\cdot x^{10}+3.21107051193712168\cdot 10^{-16}\cdot x^{12}\end{array}}}\right)\\&~&\\\operatorname {Ci} (x)&\approx &\gamma +\ln(x)+\\&&x^{2}\cdot \left({\frac {\begin{array}{l}-0.25+7.51851524438898291\cdot 10^{-3}\cdot x^{2}-1.27528342240267686\cdot 10^{-4}\cdot x^{4}+1.05297363846239184\cdot 10^{-6}\cdot x^{6}\\~~~-4.68889508144848019\cdot 10^{-9}\cdot x^{8}+1.06480802891189243\cdot 10^{-11}\cdot x^{10}-9.93728488857585407\cdot 10^{-15}\cdot x^{12}\\\end{array}}{\begin{array}{l}1+1.1592605689110735\cdot 10^{-2}\cdot x^{2}+6.72126800814254432\cdot 10^{-5}\cdot x^{4}+2.55533277086129636\cdot 10^{-7}\cdot x^{6}\\~~~+6.97071295760958946\cdot 10^{-10}\cdot x^{8}+1.38536352772778619\cdot 10^{-12}\cdot x^{10}+1.89106054713059759\cdot 10^{-15}\cdot x^{12}\\~~~+1.39759616731376855\cdot 10^{-18}\cdot x^{14}\\\end{array}}}\right)\end{array}}$

Las integrales se pueden evaluar indirectamente mediante las funciones auxiliares $f(x)$ y $g(x)$, que están definidas por:

:$\operatorname {Si} (x)={\frac {\pi }{2}}-f(x)\cos(x)-g(x)\sin(x)$		:$\operatorname {Ci} (x)=f(x)\sin(x)-g(x)\cos(x)$
or equivalently
:$f(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)+\operatorname {Ci} (x)\sin(x)$		:$g(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)-\operatorname {Ci} (x)\cos(x)$

Para $x\geq 4$, las funciones racionales de Padé que se proporcionan a continuación son aproximaciones a $f(x)$ y $g(x)$ con un error menor que 10⁻¹⁶:​

${\begin{array}{rcl}f(x)&\approx &{\dfrac {1}{x}}\cdot \left({\frac {\begin{array}{l}1+7.44437068161936700618\cdot 10^{2}\cdot x^{-2}+1.96396372895146869801\cdot 10^{5}\cdot x^{-4}+2.37750310125431834034\cdot 10^{7}\cdot x^{-6}\\~~~+1.43073403821274636888\cdot 10^{9}\cdot x^{-8}+4.33736238870432522765\cdot 10^{10}\cdot x^{-10}+6.40533830574022022911\cdot 10^{11}\cdot x^{-12}\\~~~+4.20968180571076940208\cdot 10^{12}\cdot x^{-14}+1.00795182980368574617\cdot 10^{13}\cdot x^{-16}+4.94816688199951963482\cdot 10^{12}\cdot x^{-18}\\~~~-4.94701168645415959931\cdot 10^{11}\cdot x^{-20}\end{array}}{\begin{array}{l}1+7.46437068161927678031\cdot 10^{2}\cdot x^{-2}+1.97865247031583951450\cdot 10^{5}\cdot x^{-4}+2.41535670165126845144\cdot 10^{7}\cdot x^{-6}\\~~~+1.47478952192985464958\cdot 10^{9}\cdot x^{-8}+4.58595115847765779830\cdot 10^{10}\cdot x^{-10}+7.08501308149515401563\cdot 10^{11}\cdot x^{-12}\\~~~+5.06084464593475076774\cdot 10^{12}\cdot x^{-14}+1.43468549171581016479\cdot 10^{13}\cdot x^{-16}+1.11535493509914254097\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\&&\\g(x)&\approx &{\dfrac {1}{x^{2}}}\cdot \left({\frac {\begin{array}{l}1+8.1359520115168615\cdot 10^{2}\cdot x^{-2}+2.35239181626478200\cdot 10^{5}\cdot x^{-4}+3.12557570795778731\cdot 10^{7}\cdot x^{-6}\\~~~+2.06297595146763354\cdot 10^{9}\cdot x^{-8}+6.83052205423625007\cdot 10^{10}\cdot x^{-10}+1.09049528450362786\cdot 10^{12}\cdot x^{-12}\\~~~+7.57664583257834349\cdot 10^{12}\cdot x^{-14}+1.81004487464664575\cdot 10^{13}\cdot x^{-16}+6.43291613143049485\cdot 10^{12}\cdot x^{-18}\\~~~-1.36517137670871689\cdot 10^{12}\cdot x^{-20}\end{array}}{\begin{array}{l}1+8.19595201151451564\cdot 10^{2}\cdot x^{-2}+2.40036752835578777\cdot 10^{5}\cdot x^{-4}+3.26026661647090822\cdot 10^{7}\cdot x^{-6}\\~~~+2.23355543278099360\cdot 10^{9}\cdot x^{-8}+7.87465017341829930\cdot 10^{10}\cdot x^{-10}+1.39866710696414565\cdot 10^{12}\cdot x^{-12}\\~~~+1.17164723371736605\cdot 10^{13}\cdot x^{-14}+4.01839087307656620\cdot 10^{13}\cdot x^{-16}+3.99653257887490811\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\\end{array}}$

Véase también

• Integral senoidal
• Logaritmo integral
• Seno cardinal
• Seno hiperbólico
• Coseno hiperbólico
• Tangente hiperbólica

Bibliografía

• Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [junio de 1964]. «Chapter 5». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first edición). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 231. ISBN 978-0-486-61272-0. LCCN 64060036. MR 0167642. LCCN 6512253. 

Lecturas adicionales

• Mathar, R.J. (2009). «Numerical evaluation of the oscillatory integral over exp(iπx)·x^1/x between 1 and ∞».

. 

• Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007). «Section 6.8.2 – Cosine and Sine Integrals». Numerical Recipes: The Art of Scientific Computing (3rd edición). New York: Cambridge University Press. ISBN 978-0-521-88068-8. Archivado desde el original el 11 de agosto de 2011. Consultado el 21 de enero de 2024. 
• Sloughter, Dan. «Sine Integral Taylor series proof». Difference Equations to Differential Equations. Archivado desde el original el 5 de noviembre de 2015. Consultado el 21 de enero de 2024. 
• Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., eds. (2010). NIST Handbook of Mathematical Functions. Cambridge University Press. ISBN 978-0-521-19225-5. MR 2723248. 

Enlaces externos

• http://mathworld.wolfram.com/SineIntegral.html
• Hazewinkel, Michiel, ed. (2001), «Integral trigonométrica cardinal», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
• Hazewinkel, Michiel, ed. (2001), «Integral trigonométrica cardinal», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .

• Datos: Q1094282