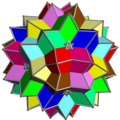
Compuesto de diez octaedros
poliedro compuesto
| Compuestos de diez octaedros | |
|---|---|
| |
| Tipo | Compuesto uniforme |
| Índice | UC15 y UC16 |
| Poliedros | 10 octaedros |
| Caras | 20+60 triángulo |
| Aristas | 120 |
| Vértices | 60 |
| Grupo de simetría | Icosaédrico (Ih) |
| Subgrupo restringido a un elemento | Antiprismático de 3 lóbulos (D3d) |
Los compuestos de diez octaedros[1] UC15 y UC16 son dos poliedros compuestos uniformes. Están formados mediante una disposición simétrica de 10 octaedros, considerados como antiprismas triangulares, alineados con los ejes de triple simetría rotacional de un icosaedro. Los dos compuestos difieren en la orientación de sus octaedros: cada compuesto puede transformarse en el otro rotando cada octaedro 60 grados.

Coordenadas cartesianas
editarLas coordenadas cartesianas de los vértices de este compuesto son todas las permutaciones cíclicas de:
- (0, ±(τ-1√2 + 2sτ), ±(τ√2 - 2sτ-1))
- (±(√2 - sτ2), ±(√2 + s(2τ - 1)), ±(√2 + sτ-2))
- (±(τ-1√2 - sτ), ±(τ√2 + sτ-1), ±3s)
donde τ = (1 + √5)/2 es el número áureo (a veces escrito φ) y s es +1 o -1. Haciendo s = -1 se obtiene UC15, mientras que cuando s = +1 se genera UC16.
Véase también
editarReferencias
editar- ↑ Skilling, John (1976), «Uniform Compounds of Uniform Polyhedra», Mathematical Proceedings of the Cambridge Philosophical Society 79: 447-457, MR 0397554, doi:10.1017/S0305004100052440..
Enlaces externos
editar- Weisstein, Eric W. «Compuesto de diez octaedros». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
