Base de datos de tablas de finales
Una base de datos de tablas de finales es una base de datos computarizada de todas las posiciones de ajedrez dentro de ciertos finales. La base de datos de tablas muestra el valor de cada posición según la teoría del juego (victoria, derrota o tablas) y cuántos movimientos tardará en conseguir ese resultado con un juego perfecto. Así, la base de datos actúa como una máquina oracle, proporcionando siempre los movimientos óptimos para las Blancas y las Negras.
Las bases de datos de tablas se generan mediante ajedrez retrospectivo, trabajando hacia atrás desde una posición de jaque mate. Las bases de datos de tablas han resuelto el ajedrez para todas las posiciones con seis o menos piezas (incluyendo los dos reyes). Los resultados de la solución han avanzado profundamente en los conocimientos de la teoría de finales por parte de la comunidad ajedrecística. Algunas posiciones que los humanos habían analizado como tablas se probó que eran ganables, la base de datos de tablas podían ver un mate en 100 movimientos o más, muy lejos del horizonte de los humanos y las computadoras. Las bases de datos han aumentado la competitividad del juego y facilitado la composición de estudios. Proporcionan una potente herramienta analítica, permitiendo a los estudiosos del ajedrez descubrir sus secretos más profundos.
Origen
editarEn principio, es posible resolver cualquier juego con la condición de que se conozca el estado completo y no haya ninguna oportunidad aleatoria. Las soluciones fuertes se conocen para algunos juegos simples, como las tres en raya (tablas con un juego perfecto) y el Conecta Cuatro (el primer jugador gana) y en julio de 2007 para las damas utilizando el "Chinook" (tablas con juego perfecto). Otros juegos como el ajedrez (desde la posición inicial) y el Go, no se han resuelto debido a que su complejidad es demasiado grande para que los ordenadores evalúen todas las posibles posiciones. Para reducir la complejidad del juego, los investigadores han modificado estos juegos complejos reduciendo el tamaño del tablero, el número de piezas o ambos.
El ajedrez por computadora es uno de los terrenos más antiguos de la inteligencia artificial, habiendo empezado en los años 1940. Claude Shannon propuso los criterios formales para evaluar los movimientos del ajedrez en 1949. En 1951, Alan Turing diseñó un programa primitivo que jugaba al ajedrez, que asignaba valores para material y movilidad, el programa "jugaba" al ajedrez basándose en los cálculos manuales de Turing (Levy y Newborn, 1991, pp. 25-38). Sin embargo, incluso cuando se empezaron a desarrollar programas de ajedrez competentes, exhibieron una debilidad manifiesta jugando los finales. Los programadores añadieron heurísticas específicas para el final, por ejemplo, el rey debería moverse al centro del tablero. Sin embargo, era necesaria una solución comprensible.
En 1965, Richard Bellman propuso la creación de una base de datos para resolver finales de ajedrez y damas utilizando ajedrez retrospectivo (Stiller1995, Stiller 1995:84).[1] En vez de analizar hacia delante a partir de la posición actual, la base de datos analizaría hacia atrás desde posiciones donde un jugador da jaque mate. Así, una computadora de ajedrez no necesitaría analizar nunca más posiciones finales durante la partida porque estarían resueltas de antemano. No volvería a haber errores porque las bases de datos de tablas siempre jugarían el mejor movimiento posible.
En 1970, Thomas Ströhlein publicó una tesis doctoral[2][3] con análisis de las siguientes clases de finales: RDR, RTR, RPR, RDRT y RTRC.[4] Ken Thompson y otros ayudaron a extender las bases de datos para cubrir todos los finales de cuatro y cinco piezas, incluyendo en particular RAARC, RDPRD y RTPRT.[5][6] Lewis Stiller publicó una tesis con investigaciones sobre algunas bases de datos de tablas de finales con seis piezas en 1995 (Stiller1995, Stiller 1995:68-113).[7]
Los contribuyentes más recientes son los siguientes:
- Eugene Nalimov por el que las base de datos de tablas de finales reciben su nombre.
- Eiko Bleicher, que ha adaptado el concepto de base de datos de tablas a un programa llamado "Freezer".
- Guy Haworth, un académico de la Universidad de Reading, que ha publicado intensivamente en el ICGA Journal.
- Marc Bourzutschky y Yakov Konoval, que han colaborado para analizar los finales con siete piezas en el tablero.
Las primeras tablas de finales para 4 piezas se construyeron al final de los años ochenta, las de 5 piezas en los 90 y el análisis de todos los finales de hasta seis piezas (incluyendo los dos reyes) se completó en 2006. (Sin embargo, las bases de datos de tablas con cinco piezas contra un solo rey no se han producido porque el resultado es casi siempre obvio.)
La investigación de bases de datos de siete piezas se estimaba que sería completada a finales de 2015.[8] pero se lograron en 2013 en Rusia gracias a un superordenador llamado Lomonósov. Debido a su origen se las conoce como tablas Lomonosov. Ocupan 140 Terabytes pero puede consultarse en la web sin ser descargadas por completo.
Generación de las bases de datos
editarMétricas: Profundidad de conversión y profundidad de mate
editarAntes de crear una base de datos de tablas, un programador tiene que elegir una métrica de optimalidad, en otras palabras, se tiene que definir en qué punto un jugador ha ganado la partida. Cada posición puede definirse por su distancia (p.ej. el número de movimientos) desde el punto final deseado. Generalmente se utilizan dos métricas:
- Profundidad del mate (DTM, del inglés Depth to mate). El mate es el único camino considerado hacia la victoria.
- Profundidad de conversión (DTC, del inglés Depth to conversion). El lado atacante también puede ganar capturando material, así convirtiendo el final en uno más simple. Por ejemplo, en el final RDRT, la conversión ocurre cuando el Blanco capture la torre Negra.
Haworth ha discutido otras dos métricas, llamadas Profundidad al Movimiento Zero(DTZ, del inglés Depth to Zeroing-Move) y Profundidad para la regla (DTR, del inglés depth by the rule). Estas métricas se corrigen para la regla de los cincuenta movimientos y se han lanzado al público unas cuantas bases de datos con estas métricas.[9]
La diferencia entre DTC y DTM se puede comprender analizando el diagrama a la derecha. Cómo debería proceder el Blanco depende de qué métrica se utilice.
| Métrica | Jugadas | DTC | DTM |
|---|---|---|---|
| DTC | 1. Dxd1 Rc8 2. Dd2 Rb8 3. Dd8 mate | 1 | 3 |
| DTM | 1. Dc7+ Ra8 2. Da7 mate | 2 | 2 |
De acuerdo con la métrica DTC, el Blanco debería capturar la torre porque "gana" inmediatamente (DTC = 1), pero le llevará dos movimientos más dar mate (DTM = 3). En contraste de acuerdo con la métrica DTM, el blanco da mate en dos movimientos, así que DTM = DTC = 2.
Esta diferencia es típica de muchos finales. Normalmente DTC es menor que DTM, pero la métrica DTM lleva al mate más rápido. Las excepciones ocurren cuando el bando defensor solo tiene el rey y en el extraño final de dos caballos y rey contra rey y peón, donde DTC = DTM porque no hay material que defender para capturar o capturar el material no es bueno. De hecho, capturando el peón defensor en el final da como resultado unas tablas.
Paso 1: Generar todas las posibles posiciones
editarUna vez que se ha elegido una métrica, el primer paso es generar todas las posiciones con un material dado. Por ejemplo, generar una base de datos de tablas DTM para el final de rey y dama contra rey (RDR), la computadora tiene que describir las únicas 40.000 posiciones legales de un array.
Levy y Newborn explicaron que el número 40.000 derivas de un argumento de simetría. El rey negro se puede situar en cualquiera de las diez casillas: a1, b1, c1, d1, b2, c2, d2, c3, d3 y d4 (ver diagrama). En cualquier otra casilla, su posición se puede considerar equivalente por simetría, rotación o reflexión. Así, un rey negro en una esquina residirá en a1, a8, h8 o h1. Multiplicando este número 10 por como mucho 64 casillas para colocar al rey blanco y entonces por como mucho 64 casillas para la dama blanca. El producto 10×64×64 = 40.960. Varios cientos de estas posiciones son ilegales, imposibles o reflexiones simétricas de otra, por lo que el número real es algo menor (Levy y Newborn, 1991, pp. 140-43)(Stiller, 1995).
Para cada posición, la base de datos evalúa la situación de forma separada si mueve el Blanco o el Negro. Asumiendo que el blanco tiene la dama, casi todas las posiciones son ganadas por el blanco, con mate forzado en no más de 10 movimientos. Algunas posiciones son tablas debido al ahogado o la inevitable pérdida de la dama.
Cada pieza adicional añadida a un final sin peones multiplica el número de posiciones únicas por un factor de aproximadamente sesenta, el número aproximado de casillas no ocupadas todavía por otras piezas.
Los finales con uno o más peones incrementan la complejidad porque se reduce el argumento de simetría. Como los peones se pueden mover hacia delante, pero no hacia atrás la rotación y la reflexión vertical del tablero produce un cambio fundamental en la naturaleza de la posición. El mejor cálculo de simetría es conseguido limitando un peón a 24 casillas en el rectángulo a2-a7-d7-d2. El resto de las piezas y peones se pueden colocar en las otras 64 casillas con respecto al peón. Así, un final con peones tiene una complejidad de 24/10 = 2.4 veces un final sin peones con el mismo número de piezas.
Paso 2: Evaluar las posiciones utilizando un análisis retrospectivo
editarTim Krabbé explica el proceso de generación de una base de datos de tablas como sigue:
"La idea es que una base de datos está compuesta de todas las posiciones posibles con un material dado. Después, una subbase de datos está compuesta por todas las posiciones donde el negro es mate. Después, una donde el blanco puede dar mate. Después, una donde el negro no puede parar al Blanco dando mate al siguiente movimiento. Después, una donde el Blanco siempre puede alcanzar una posición donde el Negro no pueda parar un mate al siguiente movimiento. Y así sucesivamente, siempre un paso más allá del mate hasta que se encuentran todas las posiciones posibles. Entonces, todas estas posiciones son enlazadas hacia atrás para dar mate según el camino más corto a través de la base de datos. Esto significa que, aparte de los movimientos 'equi-óptimos', todos los movimientos en este camino son perfectos: los movimientos del Blanco siempre conducen al mate más rápido, el movimiento del Negro siempre conducen al mate más lento."[10]
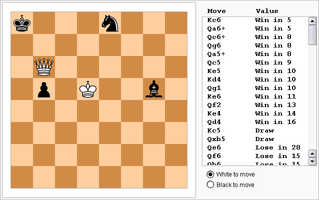
La Figura 1 ilustra la idea del análisis retrospectivo. El Blanco da mate en dos movimientos con 1.Rc6, conduciendo a la posición en la Figura 2. Entonces si 1...Rb8 2.Db7 mate y si 1...Rd8 2.Dd7 mate (Figura 3).
La Figura 3, antes del segundo movimiento del Blanco, es definida como "mate en un ply". La Figura 2, después del primer movimiento del Blanco, es "mate en dos ply" mueva lo que mueva el Negro. Finalmente, la posición inicial en la Figura 1 es "mate en tres ply" (i.e., dos movimientos) porque conduce directamente a la Figura 2, que ya está definida como "mate en dos ply". Este proceso, que enlaza una posición actual a otra posición que podría haber existido un ply antes, puede continuar indefinidamente.
Cada posición se evalúa como una victoria o una derrota en un cierto número de movimientos. Al final del análisis retrospectivo, las posiciones que no están designadas como victoria o como derrota necesariamente son tablas.
Paso 3: Verificación
editarDespués de que la base de datos se ha generado y se ha evaluado cada posición, el resultar tiene que ser verificado independientemente. El propósito es comprobar la auto-consistencia de los resultados de la base de datos.[11]
Por ejemplo, en la Figura 1 de arriba, el programa de verificación ve la evaluación "mate en tres ply (Rc6)". Entonces se observa la posición en la Figura 2, después Rc6 y se ve la evaluación "mate en dos ply". Estas dos evaluaciones son consistentes la una con la otra. Si la evaluación de la Figura 2 fuera cualquier otra, sería inconsistente con la Figura 1, con lo que la base de datos necesitaría ser corregida.
Capturas, promociones y movimientos especiales
editarUna base de datos de cuatro piezas tiene que depender de bases de datos de tres piezas que podrían dar como resultado si se captura una pieza. De la misma forma, una base de datos que contiene un peón tiene que ser capaz de depender de otras bases de datos que incluyan un nuevo conjunto de material después de una promoción de un peón a una dama u otra pieza. El programa de análisis retrospectivo tiene que tener en cuenta la posibilidad de una captura o promoción en el movimiento anterior (Stiller1995, Stiller 1995:99-100).
Las bases de datos asumen que el enroque no es posible por dos razones. Primero, en finales prácticos, esta suposición es casi siempre correcta (aunque, el enroque está permitido por convención en estudios y problemas compuestos.) Segundo, si el rey y la torre están en sus casillas originales, el enroque puede estar permitido o no. Debido a esta ambigüedad, sería necesario hacer evaluaciones separadas para estados en que el enroque es posible o no.
La misma ambigüedad existe para la captura al paso, ya que la posibilidad de una captura al paso depende del movimiento previo del oponente. Sin embargo, las aplicaciones prácticas de la captura al paso ocurren frecuentemente en finales con peones, con lo que las bases de datos toman en cuenta la posibilidad de la captura al paso para posiciones donde ambos bandos tienen al menos un peón.
Utilizando información a priori
editarDe acuerdo con el método descrito anteriormente, la base de datos tiene que permitir la posibilidad de que una pieza dada pueda ocupar cualquiera de las 64 casillas. En algunas posiciones, es posible restringir el espacio de búsqueda son afectar el resultado. Esto ahorra recursos computacionales y permite búsquedas que de otra forma serían imposibles.
Un análisis primitivo de este tipo fue publicado en 1987, en el final RTP(a2)RAP(a3), donde el alfil Negro se mueve en las casillas negras (ver posición de ejemplo a la derecha).[12] En esta posición, podemos realizar las siguientes suposiciones a priori:
- 1. Si una pieza es capturada, podemos mirar la posición resultante en la base de datos correspondiente con cinco piezas. Por ejemplo, si el peón Negro es capturado, se mira la recientemente posición creada en RTPRA.
- 2. El peón Blanco permanece en a2; los movimientos de captura son gestionados por la regla número 1.
- 3. El peón Negro permanece en a3; los movimientos de captura son gestionados por la primera regla.[13]
El resultado de esta simplificación es que, en vez de buscar 48 * 47 = 2.256 permutaciones para las ubicaciones de los peones, hay solo una permutación. Reduciendo el espacio de búsqueda por un factor de 2.256 facilita un cálculo mucho más rápido.
Bleicher ha diseñado un programa comercial llamado "Freezer", que permite a los usuarios construir nuevas bases de datos de tablas de Nalimov existentes con información a priori. El programa puede producir una base de datos para posiciones de siete piezas con peones bloqueados, incluso aunque las bases de datos de tablas no estén generalmente disponibles.[14]
Aplicaciones
editarAjedrez por correspondencia
editarEn ajedrez postal, un jugador puede consultar un ordenador de ajedrez para tener asistencia, si las reglas de la competición lo permiten. Una base de datos de seis piezas (RDDRDD) se utilizó para analizar el final de la partida por correspondencia Kasparov contra el Resto del Mundo.[15] Los jugadores también utilizan bases de datos para analizar finales en partidas en tablero en el análisis post-mortem.
Los jugadores de competición necesitan conocer que las bases de datos de tablas ignoran la regla de los cincuenta movimientos. De acuerdo con esa regla, si han pasado cincuenta movimientos sin ninguna captura o un movimiento de peón, cualquier jugador puede reclamar tablas. La FIDE ha cambiado esta regla varias veces, la primera vez en 1974, para permitir cien movimientos para finales donde cincuenta movimientos son insuficientes para ganar. En 1988, la FIDE permitió setenta y cinco movimientos para los finales RAARC, RCCRP, RDRAA, RDRCC, RTART y RDPRD con el peón en la séptima fila, porque las bases de datos de tablas habían descubierto posiciones en estos finales que necesitaban más de cincuenta movimientos para ganar. En 1992, la FIDE canceló estas excepciones y restauró la regla de los cincuenta movimientos original.[9] Así, una base de datos de tablas debe identificar una posición como ganada o perdida, teniendo en cuenta la regla de los cincuenta movimientos.
Haworth ha diseñado una base de datos de tablas que produce resultados consistentes con la regla de los cincuenta movimientos. En general, sin embargo, las bases de datos no aceptan esta restricción artificial, y buscan los límites teóricos o el mate forzado, incluso si necesita varios cientos de movimientos.
Ajedrez por ordenador
editarEl conocimiento contenido en bases de datos concede a los ordenadores una tremenda ventaja en los finales. Los ordenadores no solo juegan perfectamente un final, sino que pueden simplificar a una posición ganada en la base de datos en finales más complejos.[16] Para el último propósito, algunos programas utilizan "bases de bit" que dan el valor teórico de posiciones sin el número de movimientos hasta que se realiza el mate, es decir, solo revelan si la posición está ganada, perdida o es tablas. Algunas veces incluso este dato está comprimido y la base de bits solo revela si una posiciín está ganada o no, no haciendo diferencia entre una partida perdida o tablas.[17]
Sin embargo, algunos expertos del ajedrez por computadora han observado inconvenientes prácticos.[18] Además de ignorar la regla de los cincuenta movimientos, un ordenador en una posición difícil puede evitar el lado perdedor de una base de datos incluso si su oponente no puede ganar de forma práctica sin conocer la base de datos. Otro efecto adverso podría ser un abandono prematuro, o una línea de juego inferior que pierde con menos resistencia de la que puede ofrecer una bases de datos.
Otro inconveniente es que las bases de datos necesitan mucha memoria para almacenar los muchos miles de posiciones. Las bases de datos de Nalimov, que utilizan el estado del arte de las técnicas de compresión, necesitan 7.05 GB de disco duro para todos los finales de cinco piezas. Los finales de seis piezas necesitan aproximadamente 1.2 terabytes.[19] Las bases de datos de tablas de siete piezas de Nalimov necesitan más capacidad de almacenamiento de disco duro y de RAM para operar de la que estará disponible de forma práctica en un futuro cercano. Las bases de bits, sin embargo, ocupan mucho menos espacio. Las Shredderbases, por ejemplo, utilizadas por el programa Shredder, comprime todas las bases de datos de finales de tres, cuatro y cinco piezas en 157 MB. Esto es una mera fracción de los 7.05 GB que necesitan las bases de datos de tablas de Nalimov.[20]
Algunos ordenadores juegan mejor en general si su memoria está dedicada en vez de a finales a la función de búsqueda y evaluación. Los ordenadores modernos analizan lo suficientemente lejos convencionalmente para manejar los finales elementales sin la necesidad de bases de datos (p.ej. sin sufrir el efecto horizonte). Es solo para posiciones más sofisticadas que la base de datos mejorará significantemente sobre la computación ordinaria.
Teoría de finales
editarLas bases de datos han respondido a preguntas que han estado durante mucho tiempo sin resolver sobre su ciertas combinaciones de material eran victoria o tablas. Los siguientes resultados interesantes fueron encontrados:
- RAARC - Bernhard Horwitz y Josef Kling (1851) propusieron que el Negro puede entablar entrando en una fortaleza defensiva, pero las bases de datos demostraron una victoria general, con un máximos de DTC = 66 o 67 y DTM = 78.[21]
- RCCRP - Alexei Troitzky estableció que esto era una victoria para los caballos si el peón estaba bloqueado más allá de la línea de Troitzky. El análisis con bases de datos de tablas ha clarificado que incluso si el peón ha cruzado la línea de Troitzky, el Blanco puede algunas veces ganar forzando un zugzwang.[22] Máximo DTC = DTM = 115 movimientos.
- RCCCCRD - Los caballos ganan en el 62.5% de las posiciones, con un máximo de DTM = 85 movimientos.[23][24]
- RDTRDT - ¡A pesar de la igualdad de material, el jugador que mueve gana en el 67.74% de las posiciones![25] El máximo DTC = 92 y el máximo DTM = 117. En este final y en el de RDDRDD, el jugador que primero da jaque normalmente gana (Nunn, 2002, pp. 379, 384).
- RTCRCC y RTARCC - Friedrich Amelung había analizado estos dos finales en los años años 1900 (Stiller1995, Stiller 1995:81). Ambos finales los gana el bando fuerte en el 78 %[26] y el 95%[27] de los casos, respectivamente. La base de datos de tablas de Stiller reveló varias largas victorias en estos finales. La victoria más larga en el final RTARCC tiene DTC = 223 y DTM = 238 movimientos. Incluso más sorprendente es la posición a la derecha donde el blanco gana empezando con 1.Re6! Stiller reportó el DTC como 243 movimientos y el DTM se halló más tarde que era de 262 movimientos (Stiller1995, Stiller 1995:102-8).
Durante algunos años, esta posición tuvo el récord del mate forzado más largo generado por ordenador. Otto Blathy había compuesto un problema de "mate en 292 movimientos" ya en 1889.[28][29] Pero en mayo de 2006, Bourzutschky y Konoval descubrieron una posición RDCRTAC con un impresionante DTC de 517 movimientos. Esto era más del doble que el máximo en las tablas de Stiller, y casi 200 movimientos más que el récord previo de DTC = 330 para una posición RDACRDA_1001. Bourzutschky escribió, "Esto fue una gran sprpresa para nosotros y es un gran tributo a la complejidad del ajedrez."[30][31]
En agosto de 2006, Bourzutschky lanzó los resultados preliminares de su análisis de los siguientes finales de siete piezas: RDDPRDD, RTTPRTT y RAARCC.[11]
Estudios
editarComo muchos estudios compuestos tratan con posiciones que existen en las bases de datos, su solvencia puede ser comprobada utilizando bases de datos. Algunos estudios han sido reventados, p.ej. se ha probado su insolvencia, por medio de una base de datos de tablas. Esto puede ser porque la solución del compositor no funciona o porque hay una alternativa igualmente efectiva que el compositor no consideró. Otra manera de reventar estudios con bases de datos es un cambio en la evaluación de un final. Por ejemplo, el final de dama y alfil contra dos torres se pensaba que era tablas, pero las bases de datos han probado que es una victoria para la dama el alfil, así que casi todos los estudios basados en este final han sido desacreditados (Nunn, 2002, p. 367-68).
Por ejemplo, Erik Pogosyants compuso el estudio a la derecha, con blancas juegan y ganan. Su pretendida línea principal fue 1.Ce3 Txh2 2.O-O-O mate! Una base de datos descubrió que 1.h4 también gana para el blanco, incluso aunque el negro pueda capturar el peón. Irónicamente, la base de datos no reconoció la solución del compositor porque incluía el enroque.[32]
Aunque las bases de datos han reventado algunos estudios, han ayudado en la creación de otros. Los compositores pueden buscar bases de datos para posiciones, interesantes como zugzwang, utilizando una técnica llamada minería de datos. Para todos los finales de tres a cinco piezas y finales de seis piezas sin peones, se ha tabulado y completado una lista de zugzwangs mutuos.[33][34][35]
Ha habido alguna controversia de si se permiten los estudios compuestos con asistencia de bases de datos en torneos de composición. En 2003, el compositor de finales y experto John Roycroft resumió el debate:
"No sólo las opiniones divergen enormemente, sino que frecuentemente son defendidas con fuerza, incluso vehementemente: en un extremo está el punto de vista de que no se puede terer la certeza de que no se ha utilizado un ordenador es inútil realizar ninguna distinción, así que nosotros simplemente deberíamos evaluar un estudio en si contenido, sin hacer referencia a sus orígenes. En el otro extremo está el punto de vista de que utilizando un ratón para dejar una posición interesante desde una lista generada por ordenador no tiene sentido de la composición, por lo que deberíamos prohibir cada una de tales posiciones."[36]
El propio Roycroft está de acuerdo con el último punto de vista. Continúa:
"Sólo tenemos claro una cosa: la distinción entre la composición clásica y la composición por ordenador debería ser preservada durante tanto tiempo como sea posible: si hay un nombre asociado con un diagrama de estudio, que el nombre sea una reclamación de autoría."[36]
Mark Dvoretsky, un maestro e instructor de ajedrez, tiene un punto de vista más permisivo. Estaba acometiendo en 2006 un estudio de Harold van der Heijden, publicado en 2001, que llegaba a la posición a la derecha después de tres movimientos introductorios. El movimiento de tablas es 4.Rb4!! (y no 4.Rb5), basado en un zugzwang mutuo que puede ocurrir tres movimientos después.
Dvoretsky comenta:
"Aquí, deberíamos incidir en una cuestión delicada. Estoy seguro que esta posición única fue descubierta con la ayuda de las famosas tablas de Thompson. Es esto un 'fraude', ¿disminuyendo el logro del compositor?
"Sí, las bases de datos son un instrumento, disponible para todos hoy en día.
Sin orientación, sin duda, probablemente podríamos extraer todavía más posiciones únicas, hay algunos compositores que lo hacen regularmente. El estándar para la evaluación debería ser el resultado conseguido. Así: los milagros, basados en complejos análisis computarizados más que en su contenido de ideas agudas, son probablemente de interés sólo para ciertos ascetas."[37]
"Juega al ajedrez con Dios"
editarEn la web de los Laboratorios Bell, Ken Thompson mantiene un link al algunas de sus bases de datos. En la cabecera se lee, "Play chess with God."[38]
Considerando la larga victoria de Stiller, a Tim Krabbé se le ocurrió una nota similar:
"Un GM no sería mejor en este tipo de final que alguien que hubiera aprendido a jugar al ajedrez ayer. Es un tipo de ajedrez que no tiene nada que ver con el ajedrez, un ajedrez que nunca se podría haber imaginado sin ordenadores. Los movimientos de Stiller son impresionantes, casi dan miedo, porque sabes que son verdad, el Algoritmo de Dios. Es como si fuera revelado el Sentido de la Vida, pero no comprendieras una palabra."[10]
Nomenclatura
editarOriginalmente, una base de datos de tablas de finales se llamaba una "base de datos de finales". Este nombre apareció en EG y el ICGA Journal empezando en los años 1970 y se utiliza algunas veces hoy en día. De acuerdo con Haworth, el ICCA Journal utilizó por primera vez la palabra "base de datos de tablas" en conexión con los finales en 1995.[39] De acuerdo con esta fuente, una base de datos de tablas contiene un conjunto completo de información, pero una base de datos puede carecer de alguna información.
Haworth prefiere el término "Tabla de Finales" y lo ha utilizado en sus artículos.[40] Roycroft ha utilziado el término "oráculo de bases de datos" en su revista, EG.[41] De todas formas, la mayoría de la comunidad ajedrecística ha adoptado "base de datos de tablas de finales" como el nombre común.
Véase también
editarReferencias
editar- ↑ R. E. Bellman (Febrero de 1965). «Sobre la aplicación de la programación dinámica a la determinación del juego óptimo en ajedrez y damas». Proceedings of the National Academy of Sciences of the United States of America 53 (2): 244-246.
- ↑ T. Ströhlein (1970). Technical University of Munich, ed. Untersuchungen über kombinatorische Spiele [Traducción: Investigaciones sobre Juegos Combinatorios] Ph.D. Thesis.
- ↑ «The 'End-Papers'» (PDF). EG (52): 25. Julio de 1978. Archivado desde el original el 25 de marzo de 2009. Consultado el 1 de abril de 2007. «Niblett y Kopec describieron y posteriormente demostraron, la base de datos óptima para el final 0103 código GB.»
- ↑ T. Niblett; A. J. Roycroft (Junio de 1979). «Cómo se creó la Base de Datos de la Clase GBR.» (PDF). EG (56): 145-46. Archivado desde el original el 28 de septiembre de 2007. Consultado el 4 de mayo de 2007.
- ↑ K. Thompson (1986). «Análisis retrospectivo de ciertos finales». ICCA Journal.
- ↑ K. Thompson (mayo de 1986). «Los Programas que Genera Bases de datos de Finales» (PDF). EG (83): 2. Archivado desde el original el 28 de septiembre de 2007. Consultado el 4 de mayo de 2007.
- ↑ L. B. Stiller (1991). «Algunos Resultados de un Análisis Retrospectivo Masivamente Paralelo». ICCA Journal.
- ↑ J. Hurd; G. McC. Haworth. «Chess Endgame Data Assurance.» (PDF). Consultado el 1 de abril de 2007.
- ↑ a b G. McC. Haworth (Marzo de 2000). «Estrategias para Optimización Restringida» (PDF). ICGA Journal. Archivado desde el original el 29 de septiembre de 2007. Consultado el 1 de abril de 2007.
- ↑ a b Tim Krabbé. «"Los Monstruos de Stiller o la Perfección en el Ajedrez."». Consultado el 1 de abril de 2007.
- ↑ a b M. Bourzutschky (27 de agosto de 2006). CCRL Discussion Board, ed. «Finales de 7-piezas con peones». Consultado el 1 de abril de 2007.
- ↑ H. J. Herik; I. S. Herschberg, N. Naka (1987). «Una Base de Datos de Seis Piezas: RTP(a2)RAnP(a3)». ICGA Journal 10 (4): 163-180.
- ↑ E. Bleicher (26-08-2004.). «Construyendo Bases de Datos de Finales de Ajederz para Posicioenscon muchas Piezas utilizando Información A-priori.» (PDF). Archivado desde el original el 27 de septiembre de 2007. Consultado el 1 de abril de 2007.
- ↑ K. Müller (mayo de 2005). «Freeze!» (PDF). En ChessCafe.com, ed. Endgame Corner. Consultado el 1 de abril de 2007.
- ↑ E. V. Nalimov; C. Wirth; G. McC. Haworth (1999). «RDDRDD y la Partida Kasparov–Mundo». ICGA Journal 22 (4): 195-212.
- ↑ Steven A. Lopez (11 de noviembre de 2006). ChessBase.com, ed. «Shredderbases». Consultado el 1 de abril de 2007.
- ↑ Aaron Tay. «Una guía para Bases de Datos de Tablas de Finales». Consultado el 9 de agosto de 2007.
- ↑ A. Tay (30 de junio de 2002). «¿Se pueden utilizar las bases de datos de tablas de finales para debilitar el juego?». Consultado el 1 de abril de 2007.
- ↑ David Kirkby (12 de marzo de 2007). «Bases de Datos de Tablas de Finales». ChessDB Tutorial. Consultado el 1 de abril de 2007.
- ↑ «Shredder Computer Chess Download - Shredderbases». Archivado desde el original el 5 de julio de 2008. Consultado el 9 de agosto de 2008.
- ↑ A. J. Roycroft (1984). «Dos Alfiles contra Caballo». EG (75): 249. Archivado desde el original el 28 de septiembre de 2007. Consultado el 4 de mayo de 2007..
- ↑ D. V. Hooper (1986). «GBR Clase 0002.01». EG (83): 3. Archivado desde el original el 28 de septiembre de 2007. Consultado el 4 de mayo de 2007.
- ↑ Tim Krabbé (12 de abril de 2005). «282. Primera base de datos de finales de 7-piezas». Open Chess Diary. Consultado el 25 de marzo de 2007.
- ↑ Emil Vlasák (21 de julio de 2005). «Noticias de bases de datos de tablas de finales de 7 piezas». Consultado el 25 de marzo de 2007.
- ↑ G. McC. Haworth (Agosto de 2001). «Deshaciéndose de Piezas» (PDF). Archivado desde el original el 29 de septiembre de 2007. Consultado el 1 de abril de 2007.
- ↑ Tim Krabbé (8 de abril de 2000). «60. Juega al ajedrez con Dios». Open Chess Diary. Consultado el 13 de mayo de 2007..
- ↑ Tim Krabbé. «"Los monstruos de Stiller o la Perfección en el Ajedrez."». Consultado el 1 de abril de 2007.
- ↑ «Blathy». 21 de junio de 2003. Archivado desde el original el 30 de agosto de 2009. Consultado el 4 de mayo de 2007.
- ↑ Udo Marks. «Udo's problem pages: Mate in 292». Archivado desde el original el 11 de agosto de 2007. Consultado el 4 de mayo de 2007.
- ↑ Tim Krabbé (31 de marzo de 2006). «311. White plays and wins in 330 moves». Open Chess Diary. Consultado el 4 de mayo de 2007..
- ↑ Tim Krabbé (26 de mayo de 2006). «316. A 517-move win». Open Chess Diary. Consultado el 4 de mayo de 2007..
- ↑ Tim Krabbé (15 de septiembre de 2006). «324. Un estudio corregido». Open chess diary. Consultado el 4 de mayo de 2007.
- ↑ G. McC. Haworth; Editor: J.W.H.M. Uiterwijk (2001). «Zugzwangs Mútuos de 3-5 piezas en Ajedrez». Proceedings of the CMG 6th Computer Olympiad Computer-Games Workshop. TR CS 01-04.
- ↑ G. McC. Haworth (2001). «Las Tablas de 6 piezas de Ken Thompson». ICGA Journal.
- ↑ G. McC. Haworth; P. Karrer, J. A. Tamplin, y C. Wirth (2001). «Ajedrez de 3–5 Piezas: Máximos y Mínimos». ICGA Journal 24 (4): 225-30.
- ↑ a b A. J. Roycroft (Julio de 2003). «Editorial». EG (149): 51. Archivado desde el original el 28 de septiembre de 2007. Consultado el 4 de mayo de 2007.
- ↑ M. Dvoretsky (Julio de 2006). «Torneo de Composición de Estudios» (PDF). En ChessCafe.com, ed. The Instructor. Consultado el 1 de abril de 2007.
- ↑ Ken Thompson (21 de agosto de 2002). «Play chess with God». Archivado desde el original el 24 de enero de 2007. Consultado el 25 de marzo de 2007.
- ↑ Guy Haworth (1995). «Bases de datos de tablas y tablas». EG (137): 151. Archivado desde el original el 5 de enero de 2012. Consultado el 4 de mayo de 2007.
- ↑ La Universidad de Reading (ed.). «Publicaciones para Mr Guy Haworth». Information Systems at Reading. Archivado desde el original el 8 de septiembre de 2007. Consultado el 4 de mayo de 2007.
- ↑ Por ejemplo, en «Proposal For The Guidance Of Tourney Organisers, Composers And Judges: 0. Definitions» (PDF). EG (135): 9. Archivado desde el original el 25 de marzo de 2009. Consultado el 1 de abril de 2007.
Bibliografía
editar- Levy, David; Monty Newborn (1991). Computer Science Press, ed. Cómo Juegan las Computadoras al Ajedrez. ISBN 0-7167-8121-2.
- Nunn, John (2002). Gambit Publications, ed. Secretos de los Finales sin Peones. ISBN 1-901983-65-X.
- Stiller, Lewis Benjamin (1995), Explotando la simetría en arquitecturas paralelas, Ph.D. Thesis, Johns Hopkins University [2007-05-04]
Enlaces externos
editar- Guía para la utilización de Bases de Datos de Tablas de Finales de Aaron Tay
- Descarga de bases de datos de tablas de finales
- Sitio de distribución para bases de datos de tablas hasta seis piezas
- 3-4-5 piezas (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última). en el FTP de Robert Hyatt
- Consulta de bases de datos de tablas en la web
- Servidor web de consultas para bases de datos Nalimov de Eiko Bleicher (hasta seis piezas)
- Servidor web de consultas para bases de datos Nalimov de Lokasoft (hasta cinco piezas)
- Posiciones máximas p.ej. posiciones más largas para finales hasta cinco piezas y algunas de hasta seis piezas, compiladas por Kirill Kryukov