Usuario:MRS~eswiki/continuidad

versión personal - el artículo oficial de la enciclopedia se encuentra aquí

En matemáticas, una función  f definida sobre un intervalo I es continua si la curva que la representa, es decir el conjunto de los puntos (x, f(x)), con x en I, está constituida de un solo pedazo, en el sentido de que se puede dibujarla sin levantar el lápiz, como en figura siguiente:

El intervalo I = [-5; 9] (cifras rojas) es el dominio de definición de f, el conjunto de los valores de x para los cuales f(x) tiene sentido.
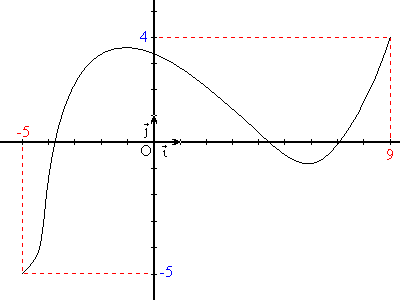
El intervalo J = [-5; 4] (cifras azules) es el codominio de f, el conjunto de los valores tomados por y = f(x). Se escribe f(I) = J. El mayor elemento de J (aquí 4) se llama el máximo de f, y el meno elemento de J (aquí -5) es su mínimo

De una manera más rigurosa se dice que una función   f es continua en un punto a si y sólo si el límite de f(x) cuando x tiende hacia a es f(a):

$f{\mbox{ es continua en }}a\Longleftrightarrow \lim _{x\to a}f(x)=f(a)$

función discontinua

La función dibujada a la derecha está definida sobre [-6 ; 6], continua sobre [-6 , 1[ ∪ ]1 ; 6], es decir que no es continua en x = 1, porque f(1) = 4 mientras que el límite a la izquierda de 1 es 3, o sea, al pasar de 1^- a 1, la función ejecuta un salto:

Una función, f es continua sobre un intervalo I, si y sólo si la función es continua en todos los puntos del intervalo, es decir:

$f{}_{es\ continua\ sobre\ I}\Longleftrightarrow \forall a\in I,\lim _{x\to a}f(x)=f(a)$

La función anterior es continua tanto en [-6 ; 1 [ como en ] 1 ; 6].

Las funciones polinomiales, las racionales, trigonométricas son continuas en sus respectivos dominios de definición.

función inversa

Resulta sorprendente, pues que cuando se habla de función discontinua, siempre se piense en la función inversa:

$f(x)={\frac {1}{x}}$,

cuya curva es una hipérbola, compuesta por dos pedazos (para x < 0 y para x > 0 ).
Esta función no está definida en 0 y, por tanto, su dominio de definición es: ]- ∞,0[ ∪ ]0,+ ∞[, y en cada intervalo, ]-∞,0[ ó ]0,+∞[, es continua.
Por consiguiente la función inversa es continua.

Lo mismo sucede con las otras funciones racionales:
los puntos de aparente discontinuidad corresponden a valores de la variable que no pertenecen al dominio de definición de la función.

parte entera

La función discontinua la más sencilla es la parte entera, E, que se define de la siguiente forma:

E(x) = [x], donde [x] es el mayor número entero inferior o igual a x, tal que, E(x) ≤ x < E(x) + 1.

Su curva es una sucesión de segmentos horizontales a distintas alturas (ver figura).
Esta función no es continua en los enteros, pues los límites a la izquierda y a la derecha difieren de uno, pero es continua en los segmentos abiertos ]n; n+1[ donde es constante.

Existen funciones que no son continuas en ningún punto: La más conocida es la función característica de $\mathbb {Q}$, es decir la función que toma como valor 1 cuando x pertenece al conjunto de los racionales, y 0 si no.
Obviamente, no se puede dibujar su curva, que está constituida por una infinidad de puntos en la recta y = 0 , y una infinidad (menor) de puntos en la recta y = 1.

continuidad en R

La definición exacta de la continuidad hace intervenir la topología de $\mathbb {R}$, más concretamente los intervalos abiertos:

Si f(a)= b, la continuidad en a se expresa así:

lim_x→a f(x) = b, parafraseando, cuando x se aproxima a a, f(x) se aproxima a b.

Por definición de los límites, esto significa que para todo intervalo abierto J centrado en b (en rojo en la figura), existe un intervalo abierto I centrado en a (en azul) tal que f(I) c J.

Si f ejecuta un salto (en el punto (c,d) de la figura) el teorema cae en falta: En efecto si se toma un intervalo J centrado en d (en amarillo) con un radio inferior al salto de f, todo intervalo I (en verde) alrededor de c, no importa cuan pequeño es, tiene una imagen que sale de J.

La ventaja de esta definición es que se generaliza a cualquier espacio topológico.

Autor: M.Romero Schmidtke