Teorema de Carnot
En geometría, el teorema de Carnot, nombrado así por el matemático francés Lazare Carnot (1753-1823), es el siguiente:
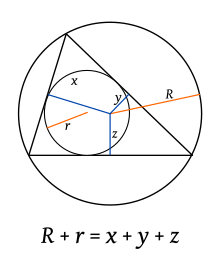

Sea ABC un triángulo cualquiera. Entonces la suma de las distancias desde el circuncentro D a los lados del triángulo ABC es
donde r es el radio del círculo inscrito en el triángulo y R es el radio del círculo circunscrito del triángulo. Aquí, el signo de la distancia es negativa si, y solo si el segmento DX (X = F, G, H) esta completamente fuera del triángulo. En la imagen de abajo (el caso de un triángulo obtusángulo) DF es negativo y los segmentos DG y DH son positivos.
Un resultado relacionado con el teorema de Carnot es el primer teorema de Mikami-Kobayashi o teorema japonés de polígonos concíclicos.
Historia
editarEn 1800, un samurai anónimo colgó en la pared de un templo una tablilla de madera en la que estaba grabado un sangaku, problema de geometría dedicado a una deidad (kami) y propuesto a la sagacidad de los fieles.
En 1803, Carnot publicó su Géométrie de position. Accidente de la historia, un teorema de este libro[1] permite elegantemente resolver el sangaku antes mencionado.
Referencias
editar- ↑ Carnot, L. N. M. (1803). Géométrie de position. J. B. M. Duprat. p. 168.
