Reacción mecánica
En ingeniería estructural e ingeniería mecánica, una reacción es una fuerza de sujeción de un elemento resistente al suelo u otro elemento de grandes dimensiones que sirve de soporte al elemento resistente. En sentido general a veces se habla de momentos de empotramiento o momentos reacción, en el caso de enlaces que además impiden el giro de algunas secciones de unión.
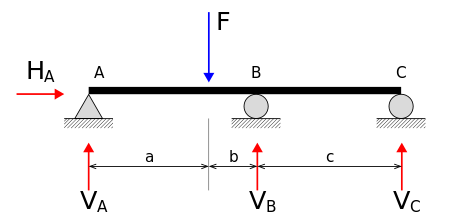
Métodos de cálculo de reacciones
editarEl cálculo de reacciones involucra calcular un número de parámetros (fuerzas o momentos) es mayor o igual que el número de grados de libertad eliminen las uniones con el exterior de una estructura o mecanismo.
Si el número de reacciones incógnita es inferior a tres el elemento resistente considerado es un mecanismo y requiere en general un cálculo dinámico para determinar completamente las reacciones. Si el número de reacciones incógnita es igual a tres, tenemos una estructura externamente isostática y las ecuaciones de la estática son suficientes para determinar las reacciones. Cuando el número de reacciones es superior a tres, tenemos una estructura hiperestática y es necesario considerar la rigidez de la misma para poder determinar completamente las reacciones. En este último caso existen diversos métodos para determinarlas:
Condición de equilibrio
editarDado un sólido una condición necesaria para que este sólido esté en equilibrio mecánico es que la suma de reacciones y el momento resultante de estas reacciones sea cero:
Si el sólido es indeformable la condición además de necesaria es suficiente, sin embargo, para ciertos sólidos deformables la condición de que la suma de fuerzas y momentos se anule puede no ser suficiente. En ese último caso además deben satisfacerse locamente las ecuaciones diferenciales de equilibrio:
Donde:
- denotan las componentes del tensor de tensiones.
- es la fuerza por unidad de volumen actuante en cada punto del sólido.
Las condiciones anteriores también son aplicables a un fluido y para la mayoría de fluidos admiten las ecuaciones anteriores son equivalentes a una forma más simple.
Referencias
editar- Marion & Thornton, Classical Dynamics of Particles and Systems. Fourth Edition, Harcourt Brace & Company (1995). (en inglés)