Raíz cúbica

La raíz cúbica,(∛) en el sistema de los números reales, estrictamente, es la función inversa de la función $y=x^{3}$ (potencia de tercer grado). La extracción de la raíz cúbica de cualquier número real puede admitirse como una operación unaria de los reales en los reales.^[1]^[2]

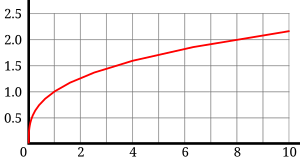
La operación de calcular la raíz cúbica se puede efectuar, sin restricciones, en el campo ordenado de los números reales, ciertamente, con aproximaciones decimales prefijadas en la mayoría de los casos. Es asociativa con la potenciación y distributiva respecto la multiplicación y división de números reales, pero no es asociativa ni distributiva con la adición o la resta. La raíz cúbica mantiene el signo del radicando.

Históricamente, el famoso problema de la duplicación del cubo, estudiado por Arquitas de Tarento, planteó la solución a través de la raíz cúbica de 2. Esta cuestión no se resolvió con la aritmética de los números racionales, tampoco con la construcción geométrica a través de regla y compás.^[3]

Para facilitar el cálculo de la raíz cúbica, se hacía uso de logaritmos y sus propiedades sobre las raíces usando tablas y también mediante la regla de cálculo; En la actualidad, se trabaja con las calculadoras.^[4]

Definición formal

Representación compleja de la raíz cúbica.

Las raíces cúbicas de un número x son números y que satisfacen la ecuación

Números reales

Si x e y son reales, entonces existe una única solución tal que la ecuación tiene además una única solución, y ésta corresponde a un número real. Si se emplea esta definición, la raíz cúbica de un número negativo es también un número negativo. De esta forma, la raíz cúbica de x es representada igualmente por:

Si x e y son ambos complejos, entonces se puede decir que posee tres soluciones (si x es no nulo) y así x tiene tres raíces cúbicas: una raíz real y dos complejas, en la forma de par conjugado. Este hecho deja interesantes resultados dentro de las matemáticas. Por ejemplo, las raíces cúbicas del número uno son:

{\sqrt[{3}]{1}}={\begin{cases}\ \ 1\\-{\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i\\-{\frac {1}{2}}-{\frac {\sqrt {3}}{2}}i\end{cases}}

Estas dos raíces se relacionan con todas las otras raíces cúbicas de otros números. Si un número es raíz cúbica de un número real las raíces cúbicas pueden ser calculadas multiplicando el número por las raíces de la raíz cúbica de uno.^[5]

Números complejos

En el cuerpo de los números complejos, la raíz cúbica responde a la solución de la ecuación

z^{3}-a=0

donde a es cualquier número complejo no nulo. El conjunto solución involucra tres valores distintos; si z es un complejo real uno de los valores es número real; los otros dos son complejos, sin ninguna parte nula.^[6]

Para los números complejos, el valor principal de las raíces cúbicas se define como:

z^{1 \over 3}=\exp \left({\operatorname {Log} {z} \over 3}\right)

Donde Log(z) es la rama principal del logaritmo complejo. Si se escribe z como

z=r\exp(i\theta )\,

Donde r es un número real positivo y $\theta$ cae en el rango:

-\pi <\theta \leq \pi

,

entonces la raíz cúbica es

{\sqrt[{3}]{z}}={\sqrt[{3}]{r}}\exp \left({i\theta  \over 3}\right)

.

Esto significa que en coordenadas polares al tomar la raíz cúbica de un número complejo se está tomando la raíz cúbica del radio y el ángulo polar se está dividiendo en tres partes de tal forma que define las tres raíces. Con esta definición, la raíz cúbica de un número negativo es un número complejo, y por ejemplo ${\sqrt[{3}]{-8}}$ no será -2, sino $1+i{\sqrt {3}}$ . En aquellos programas que aceptan resultados imaginarios (tales como Mathematica), el grafo de la raíz cúbica de x en el plano de los números reales dará como resultados valores negativos de la raíz por igual.

Números cuaterniónicos

Al igual que sucede con la raíz cuadrada de números cuaterniónicos, sucede que un número cuaterniónico puede admitir infinitas raíces cúbicas. Esto contrasta con el caso de los reales y complejos, donde por ejemplo -1 tiene un número finito de raíces cúbicas (una en los reales y tres en los complejos). Sin embargo, en los números cuaterniónicos $\scriptstyle \mathbb {H}$ hay un número infinito de raíces cúbicas de -1. Para ver esto, sea q = a + bi + cj + dk un cuaternión, y supóngase que su cubo es −1:

(a+bi+cj+dk)^{3}=-1\Rightarrow a[a^{2}-3(b^{2}+c^{2}+d^{2})]+[3a^{2}-(b^{2}+c^{2}+d^{2})](bi+cj+dk)=-1

En términos de a, b, c y d esa asunción implica que

$[a^{2}-3(b^{2}+c^{2}+d^{2})]a=-1,$

$[3a^{2}-(b^{2}+c^{2}+d^{2})]b=0,$

$[3a^{2}-(b^{2}+c^{2}+d^{2})]c=0,$

$[3a^{2}-(b^{2}+c^{2}+d^{2})]d=0.$

Una posible solución es $a=-1,b=c=d=0$ pero además de esta existe un número infinito de soluciones adicionales que juntas forman la superficie de una 2-esfera de radio ${\sqrt {3}}/2$ contenida $\mathbb {R} ^{4}\approx \mathbb {H}$ . Esto se puede ver tomando $b,c,d$ de manera que $b^{2}+c^{2}+d^{2}=3a^{2}$ (ecuación de una 2-esfera), así se cumplen las tres últimas ecuaciones. Subtsituyendo esto en la primera, vemos que esta también se satisface si $a=1/2$ :

$[a^{2}-3(b^{2}+c^{2}+d^{2})]a=[a^{2}-3(3a^{2})]a=-8a^{3}=-1\qquad \Rightarrow a=1/2$

Por tanto, queda demostrado que la ecuación $q^{3}=-1$ admite infinitas soluciones en $\mathbb {H}$

Métodos numéricos

El método de Newton es un método iterativo que puede ser usado para calcular la raíz cúbica. Para números reales representados mediante coma flotante, este método se reduce al siguiente método iterativo para producir sucesivas mejores aproximaciones de la raíz cúbica de a:

x_{n+1}={\frac {1}{3}}\left({\frac {a}{x_{n}^{2}}}+2x_{n}\right).

Si se toma $x_{1}$ por exceso $x_{1}>{\sqrt[{3}]{a}}$ la sucesión anterior es monótona decreciente y su límite es precisamente la raíz cúbica. Por ejemplo si $a=30$ , tomando $x_{1}=4$ , ya que $4^{3}>30$ ; se obtiene: