Proyección mariposa de Waterman
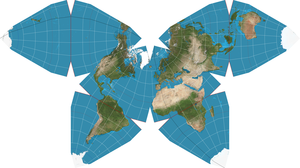
La proyección mariposa de Waterman es una proyección cartográfica creada por el matemático Steve Waterman, quien publicó por primera vez un mapa bajo esta proyección en 1996. La proyección es el despliegue de un globo terráqueo tratado como un octaedro truncado, evocando el principio del mapa de mariposa desarrollado por primera vez por Bernard Cahill en 1909. Los mapas de Cahill y Waterman pueden ser mostrados en varios perfiles, típicamente vinculados en los océanos Pacífico norte o Atlántico norte.

Como Cahill era arquitecto, su enfoque tendía hacia formas que podían demostrarse físicamente, como su mapa plano de pelota de goma. Waterman, por otro lado, derivó su diseño de su trabajo en el empaquetado de esferas. Esto implica conectar los centros de las esferas de las esferas cúbicas más cercanas en un casco convexo correspondiente.
Para proyectar la esfera al poliedro, la Tierra se divide en 8 octantes. Cada meridiano se dibuja como tres segmentos de línea recta en su octante respectivo, cada segmento definido por sus puntos finales en dos de las cuatro "Delineaciones de líneas iguales" definidas por Waterman. Estas delineaciones de líneas iguales son el Polo Norte, el borde del poliedro más septentrional, la línea más larga paralela al ecuador y el ecuador mismo. Las intersecciones de todos los meridianos con una delineación de línea igual están igualmente espaciadas, y las intersecciones de todos los paralelos con cualquier meridiano están igualmente espaciadas.[1] Waterman eligió el meridiano central de 20° O para minimizar la interrupción de las grandes masas de tierra. La proyección también puede ser gnomónica.[2] Los dos métodos arrojan resultados muy similares.
Al igual que la Proyección Dymaxion de 1943 de Buckminster Fuller, un mapa de mariposa octaédrica puede mostrar todos los continentes sin interrupción si sus octantes se dividen en un meridiano adecuado (en este caso 20° O) y se unen, por ejemplo, en el Atlántico Norte.
Referencias
editar- ↑ «Waterman Projection Method» (en inglés). Consultado el 23 de enero de 2020.
- ↑ Popko, Edward (2012). «Bucky's dome». Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere (en inglés). Boca Raton: CRC Press. pp. 20-21. ISBN 978-1-4665-0429-5. Consultado el 23 de enero de 2020.
Enlaces externos
editar- Esta obra contiene una traducción parcial derivada de «Waterman butterfly projection» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.