Producto libre de grupos
En las matemáticas, particularmente en la teoría de grupos, el producto libre de grupos es la construcción de un nuevo grupo a partir de una dada colección de ellos y que permite la inclusión como subgrupos a cada uno de los factores que le construyen.
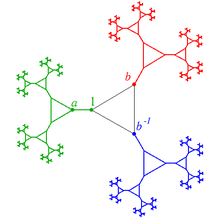
Para ilustrar la construcción, más precisamente, utilicemos dos grupos G, H. Entonces su producto libre es el grupo que consiste en un nuevo grupo cuyos elementos tienen la forma canónica
donde los y los es decir los elementos de G*H son palabras reducidas de letras alternadas que son elementos de los dos grupos G y H respectivamente.
Entonces uno puede pensar que el grupo G está incluido en G*H pues trivialmente vemos que cada elemento de G es una palabra reducida en G*H, y similarmente para H.
Un ejemplo básico es el grupo libre, de rango dos; este, se puede interpretar como
Otro un poco más complejo es que se interpreta como
Generalizaciones
editarUna manera similar pero más general de construir grupos a partir de antiguos es el producto libre amalgamado, que consiste empezar con dos grupos arbitrarios A, B y un tercer C que se encuentra encajado en ambos A y B, entonces uno toma el cociente a partir del producto libre de A con B y haciendo módulo N(C) que es la clausura normal de C en ambos A, B.
En símbolos matemáticos se acostumbra a escribir al producto libre de A con B amalgamados por C como:
Ejemplos de esta construcción aparecen en el teorema de Seifert-van Kampen donde se calcula es grupo fundamental de un espacio topológico en términos de los grupos fundamentales de algunos de sus subespacios.
Referencias
editar- libro de Ross Geoghegan: Topological methods in group theory, GTM-243 (2008), Springer ISBN 978-0-387-74611-1.
- panfleto de Peter Scott y Terry Wall titulado: Topological methods in group theory, London Math. Soc. Lecture Note Ser., 36, Cambridge Univ. Press (1979) 137-203. En dirección [1], en el apartado de sources for the Bass Serre theory puedes descargarlo.







