Politopo semirregular
| Panales 3D | ||
|---|---|---|
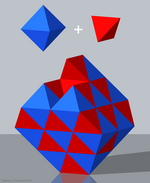 Control tetraédrico simple |
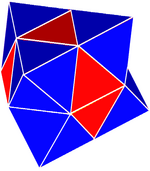 Control tetroctaédrico complejo | |
| 4D-politopos | ||
 Tetroctaédrico |
 Octicosaédrico |
 Tetricosaédrico |
En geometría, según la definición del matemático británico Thorold Gosset (1869-1962), de forma general se considera un politopo semirregular a un tipo de politopo que es vértices-transitivo y tal que todas sus facetas son politopos regulares.[1] E.L. Elte compiló en 1912 una lista ampliada titulada "Los politopos semirregulares de los hiperespacios", que incluía una definición más completa.[2] Para denominar los nuevos politopos encontrados, Gosset utilizó el término check (aquí traducido como "control").
Lista de Gosset
editarEn el espacio tridimensional y en espacios de dimensiones inferiores, los términos politopo semirregular y politopo uniforme tienen significados idénticos, dado que todos los polígonos uniformes deben ser regulares. Sin embargo, dado que no todos los poliedros uniformes son regulares, el número de politopos semirregulares en dimensiones superiores a tres es mucho menor que el número de politopos uniformes en el mismo número de dimensiones.
Los tres polícoros semirregulares convexos son el 5-celdas rectificado, el 24-celdas romo y el 600-celdas rectificado. Los únicos politopos semirregulares en dimensiones superiores son los politopos k21, donde el de 5 celdas rectificado es el caso especial para k = 0. Todos fueron enumerados por Gosset, pero no se publicó una prueba de la integridad de esta lista hasta el trabajo de Makarov (1988) para cuatro dimensiones y Blind y Blind (1991) para dimensiones superiores.
Los 4-politopos de Gosset (con sus nombres entre paréntesis), son:
- 5-celdas rectificado (tetroctaédrico),
- 600-celdas rectificado (octicosaédrico),
- 24-celdas romo (tetricosaédrico), , o
E-politopos semirregulares en dimensiones superiores:
- 5-demicubo (5-ic semirregular), un 5-politopo, ↔
- Politopo 221 (6-ic semirregular), un 6-politopo, o
- Politopo 321 (7-ic semirregular), un 7-politopo,
- Politopo 421 (8-ic semirregular), un 8-politopo,
Panales euclídeos
editarLos politopos semirregulares se pueden extender a panales semirregulares. Los panales euclídeos semirregulares son el panal tetraédrico-octaédrico (3D), el panal cúbico alternado girado (3D) y el panal 521 (8D).
Panales de Gosset:
- Panal tetraédrico-octaédrico o panal cúbico alternado (control tetroctaédrico simple), ↔ (también cuasirregular)
- Panal cúbico alternado girado (control tetroctaédrico complejo),
Panales euclídeos semirregulares:
- Panal 521 (control 9-ic) (panal euclídeo 8D),
Gosset (1900) además consideró la disposición de panales euclídeos como facetas de otros panales euclídeos de dimensiones superiores, dando las siguientes figuras adicionales:
- Prisma de panal hipercúbico, denominado por Gosset como semi-control (n – 1)-ic (análogo a una sola fila o columna de un tablero de ajedrez)
- Panal de teselas hexagonales alternado (semi-control tetraédrico),
Panales hiperbólicos
editarTambién hay panales uniformes hiperbólicos compuestos únicamente por celdas regulares (Coxeter y Whitrow, 1950), que incluyen:
- Panales uniformes hiperbólicos, panales 3D:
- Panales uniformes paracompactos, panales 3D, que incluyen teselados uniformes como celdas:
- Panal tetraédrico de orden-6 rectificado,
- Panal teselado cuadrado rectificado,
- Panal teselado cuadrado de orden-4 rectificado, ↔
- Panal cúbico de orden-6 alternado, ↔ (también cuasirregular)
- Panal teselado hexagonal alternado, ↔
- Panal teselado hexagonal de orden-4 alternado, ↔
- Panal teselado hexagonal de orden-5 alternado, ↔
- Panal teselado hexagonal de orden-6 alternado, ↔
- Panal teselado cuadrado alternado, ↔ (también cuasirregular)
- Panal teselado cúbico-cuadrado,
- Panal teselado cuadrado de orden-4, =
- Panal teselado tetraédrico-triangular,
- Panal paracompacto hiperbólico 9D:
- Panal 621 (control 10 ic),
Véase también
editarReferencias
editar- ↑ H. S. M. Coxeter (2012). Regular Polytopes. Courier Corporation. p. 368. ISBN 9780486141589. Consultado el 1 de septiembre de 2023.
- ↑ Peter McMullen, Egon Schulte (2002). Abstract Regular Polytopes, Volumen 92. Cambridge University Press. pp. 526 de 551. ISBN 9780521814966. Consultado el 1 de septiembre de 2023.
Bibliografía
editar- Blind, G.; Blind, R. (1991). «The semiregular polytopes». Commentarii Mathematici Helvetici 66 (1): 150-154. MR 1090169. S2CID 119695696. doi:10.1007/BF02566640.
- Coxeter, H. S. M. (1973). Regular Polytopes (3rd edición). New York: Dover Publications. ISBN 0-486-61480-8.
- Coxeter, H. S. M.; Whitrow, G. J. (1950). «World-structure and non-Euclidean honeycombs». Proceedings of the Royal Society 201 (1066): 417-437. Bibcode:1950RSPSA.201..417C. MR 0041576. S2CID 120322123. doi:10.1098/rspa.1950.0070.
- Elte, E. L. (1912). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X.
- Gosset, Thorold (1900). «On the regular and semi-regular figures in space of n dimensions». Messenger of Mathematics 29: 43-48.
- Makarov, P. V. (1988). «On the derivation of four-dimensional semi-regular polytopes». Voprosy Diskret. Geom. Mat. Issled. Akad. Nauk. Mold. 103: 139-150, 177. MR 958024.