Período orbital
El período orbital es el tiempo que le toma a un astro recorrer su órbita. Cuando se trata de objetos que orbitan alrededor del sol existen dos tipos:
- El período sideral es el tiempo que tarda el objeto en dar una vuelta completa alrededor del sol, tomando como punto de referencia una estrella fija. Se considera el auténtico período orbital del objeto y sería el que vería un observador inmóvil que no orbitara alrededor del sol.
- El período sinódico es el tiempo que tarda el objeto en volver a aparecer en el mismo punto del cielo respecto al sol, cuando se observa desde la Tierra. Este período tiene en cuenta que la Tierra, lugar desde el cual es observado el objeto, también orbita en torno al sol. Es, por tanto, el tiempo que transcurre entre dos conjunciones sucesivas con el sol, y es el período orbital aparente.
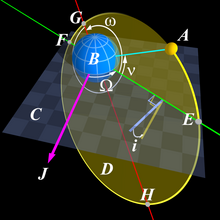
El período sideral y el sinódico difieren, ya que la Tierra, a su vez, da vueltas alrededor del Sol.
Otros períodos relacionados con el período orbital
editarHay muchos períodos relacionados con las órbitas de los objetos, cada uno de los cuales se utilizan a menudo en los diversos campos de la astronomía y la astrofísica. Ejemplos de algunos de los más comunes son:
El período sideral es la cantidad de tiempo que toma un objeto para hacer una órbita completa, en relación con las estrellas. Este es el período orbital en un marco de referencia inercial (no giratorio).
El período sinódico es la cantidad de tiempo que tarda un objeto en reaparecer en el mismo punto en relación con dos o más objetos (por ejemplo, la fase lunar y su posición respecto al Sol y la Tierra se repiten cada 29,5 días sinódicos, más largos que su órbita de 27,3 días alrededor de la Tierra, debido al movimiento de la Tierra alrededor del Sol). El tiempo entre dos oposiciones o conjunciones sucesivas es también un ejemplo de período sinódico. Para los planetas del sistema solar, el período sinódico (con respecto a la Tierra) difiere del período sideral debido a la órbita de la Tierra alrededor del Sol.
El período draconiano o período dracónico es el tiempo que transcurre entre dos pasajes del objeto a través de su nodo ascendente, el punto de su órbita donde cruza la eclíptica desde el hemisferio sur hasta el hemisferio norte. Este período difiere del período sideral porque tanto el plano orbital del objeto como el plano del preceso eclíptico se separan con respecto a las estrellas fijas, por lo que su intersección, la línea de nodos, también precesa con respecto a las estrellas fijas. Aunque el plano de la eclíptica a menudo se mantiene fijo en la posición que ocupaba en una época específica, el plano orbital del objeto todavía precesa, haciendo que el período draconítico difiera del período sideral.
El período anomalístico es el tiempo que transcurre entre dos pasajes de un objeto en su periapsis (en el caso de los planetas del sistema solar, llamado perihelio), el punto de su aproximación más cercana al cuerpo atrayente. Se diferencia del período sideral porque el eje semi-mayor del objeto suele avanzar lentamente.
Además, el período tropical de la Tierra (o simplemente su "año") es el tiempo que transcurre entre dos alineaciones de su eje de rotación con el Sol, también vistas como dos pasajes del objeto en la ascensión recta cero. Un año terrestre tiene un intervalo ligeramente más corto que la órbita solar (período sideral) debido a que el eje inclinado y el plano ecuatorial avanzan lentamente (giran con respecto a las estrellas), realineándose con el Sol antes de que la órbita se complete. El ciclo de precesión de la Tierra se completa en unos 25 770 años.
Cálculo estándar del periodo orbital
editarUn cuerpo pequeño orbitando un cuerpo central
editarDada una órbita circular o elíptica alrededor de un objeto masivo central, la tercera ley de Kepler, el periodo orbital T (en segundos) viene dado por:
donde:
- es el semi-eje mayor de la órbita (en metros).
- es el parámetro gravitacional estándar en m³ s-2
- G es la constante gravitacional. .
- M es la masa del objeto más masivo.
Obsérvese que este periodo es válido para todas las órbitas cerradas, es decir, circulares y elípticas, sin importar su excentricidad.
Inversamente podemos calcular el semi-eje mayor de una órbita dado su periodo orbital con la siguiente expresión:
Podríamos por ejemplo calcular un caso curioso aunque poco viable en la práctica. Si quisiéramos hacer orbitar un objeto ligero en torno a una masa de 100 kg con un periodo de 24 horas en una órbita circular, el radio de la misma debería ser de 1.08 metros.
Dos cuerpos orbitándose el uno al otro
editarEn la mecánica celeste, cuando hay que tener en cuenta las masas de ambos cuerpos orbitales, el período orbital T puede calcularse de la siguiente manera:[1]
donde:
- a es la suma de los ejes semimayores de las elipses en las que se mueven los centros de los cuerpos, o equivalente, el eje semimayor de la elipse en la que se mueve un cuerpo, en el marco de referencia con el otro cuerpo en el origen (que es igual a su separación constante para órbitas circulares),
- M1 + M2 es la suma de las masas de los dos cuerpos,
- G es la constante gravitacional.
Tenga en cuenta que el período orbital es independiente del tamaño: para un modelo a escala sería el mismo, cuando las densidades son las mismas (véase también Orbit § Scaling in gravity).
En una trayectoria parabólica o hiperbólica, el movimiento no es periódico, y la duración de la trayectoria completa es infinita.
Cálculo del periodo sideral
editarSuponiendo órbitas completamente circulares, la Tierra se movería 360° en un tiempo T de 365.2425 días, mientras que el astro se movería 360° en un tiempo P (periodo sideral o real). Eso es igual al tiempo S (periodo sinódico o aparente) más una compensación por ir más o menos rápido que la Tierra. Se obtiene por lo tanto la siguiente ecuación:
El signo de ±360° es una suma si el astro da una vuelta a su órbita en menor tiempo que la Tierra —sea un planeta interior (diferente a Marte o la propia Tierra) o la Luna—, es una resta si el astro da una vuelta a su órbita en mayor tiempo que la Tierra —sea Marte, un planeta exterior o un planeta enano—.
Simplificando y despejando, usando el álgebra, obtenemos la siguiente fórmula:
De la que si despejamos el período sinódico S obtenemos éste en función de los períodos sidéreos de la Tierra T y del planeta P
Los períodos sinódicos de los 7 planetas son: de 115,88 días para Mercurio, 583,92 días Venus, 779,94 días Marte, 398,88 días Júpiter, 378,09 Saturno, 369,66 días Urano y 367,49 días Neptuno.
Y si lo que queremos calcular es el período sidéreo P del planeta conocidos su período sinódico S y el período sidéreo de la Tierra T la expresión es:
Comprobación
editarPara comprobar la validez del cálculo del período sidéreo a partir del período sinódico usaremos un caso real: la Luna. Si estamos en la Tierra y observamos la luna a través de los días veremos que tarda aproximadamente 29 d 12 h 44 min en su periodo sinódico (aparente desde la Tierra con respecto al sol) o bien 29.530556 días, lo cual es el valor de S. Sabemos que la Tierra tarda aproximadamente 365.256363 días en dar una vuelta al sol,[2] lo cual será nuestro valor T. La operación queda así:
El signo es positivo dado que da una vuelta a su propia órbita más rápido que la Tierra a la suya. El resultado es redondeado con seis decimales. Es el valor de 1/P y para obtener P (periodo sideral o real, de la luna en este caso) solo hacemos la operación 1÷0.036601 = 27.321659 días.
Sabemos que el periodo sideral de la luna es de aproximadamente 27 d 7 h 43 min o 27.321529 días, por lo que nuestro resultado se aproxima mucho al valor real.
Períodos de revolución sideral de los principales cuerpos del Sistema Solar
editarPlanetas
editar- Mercurio: ~87,969 256 días[3] (~88 días~)
- Venus: ~ 224,699 705 6 días[3] (~225 días~)
- Tierra: ~ 365,256 363 051 días[3] (1 año)
- Marte: ~ 686,979 852 días[3] (~ 1 año +321 días~)
- Júpiter: ~4.332,589 días[3] (~11 años +315 días)
- Saturno: ~ 10.759,23 días[3] (~ 29 años + 167 días~)
- Urano: ~ 30.685,4 días[3] (~ 84 años)
- Neptuno: ~60.266 días[3] (~164 años + 280 días)
Planetas enanos y candidatos
editarPeríodos orbitales en número de rotaciones
editarLa siguiente tabla indica la duración de una revolución alrededor del Sol (un año) en número de rotaciones de la cuerpos (número de "días" del cuerpo en cuestión).
Téngase en cuenta que el año terrestre corresponde a 366.256 rotaciones y no a 365.256 (año sidéreo), porque la duración de un día solar corresponde a un poco más de una rotación. En efecto, para que el Sol vuelva al meridiano local (es decir, para que transcurra un día solar), la Tierra debe hacer un poco más de una rotación, porque durante este tiempo ha girado alrededor del Sol, y el Sol ya no está en la misma dirección con respecto a ella.
| Cuerpo | Periodo de rotación
(en días terrestres) |
Periodo orbital
(en días terrestres) |
Periodo orbital
(en número de rotaciones) |
|---|---|---|---|
| Mercurio | 58,65 días | 87,96 días | 1,499 rotaciones |
| Venus | 243,01 días | 224,69 días | 0,924 rotaciones |
| Tierra | 23,934 horas | 365,256 días | 365,256 rotaciones |
| Marte | 24,630 horas | 686,97 días | 669,407 rotaciones |
| Júpiter | 9,841 horas | 4332,589 días | 10 566,21 rotaciones |
| Saturno | 10,233 horas | 10 759,23 días | 25 234,19 rotaciones |
| Urano | 17,9 horas | 30 685,4 días | 41 142,43 rotaciones |
| Neptuno | 16,11 horas | 60 216,8 días | 89 708,45 rotaciones |
| Ceres | 9,07 horas | 1680 días | 4445,42 rotaciones |
| Plutón | 6,387 días | 90 588 días | 14 183,18 rotaciones |
| Sedna | 10,273 horas | 4 313 319 días | 10 078 867 rotaciones |
| Makemake | 22,83 horas | 112 000 días | 117 739,81 rotaciones |
| Eris | 25,9 horas | 203 450 días | 188 525,09 rotaciones |
Véase también
editarReferencias
editar- ↑ Bradley W. Carroll, Dale A. Ostlie. An introduction to modern astrophysics. 2nd edition. Pearson 2007.
- ↑ Staff (7 de agosto de 2007). «Useful Constants» (en inglés). International Earth Rotation and Reference Systems Service. Consultado el 23 de septiembre de 2008.
- ↑ a b c d e f g h i «Planetary Fact Sheet - Metric». NASA (en inglés).
Enlaces externos
editar- «Video que resume la rotación de la Tierra (Vidéo résumant la rotation de la Terre)». YouTube (en francés). Consultado el 8 de noviembre de 2023.