Perceptrón

En el campo de las Redes Neuronales, el perceptrón, creado por Frank Rosenblatt,^[1] se refiere a:

la neurona artificial o unidad básica de inferencia en forma de discriminador lineal, a partir de lo cual se desarrolla un algoritmo capaz de generar un criterio para seleccionar un subgrupo a partir de un grupo de componentes más grande.

La limitación de este algoritmo es que si dibujamos en un gráfico estos elementos, se deben poder separar con un hiperplano únicamente los elementos «deseados» discriminándolos (separándolos) de los «no deseados».

El perceptrón puede utilizarse con otros tipos de perceptrones o de neurona artificial, para formar una red neuronal artificial más compleja.

Definición

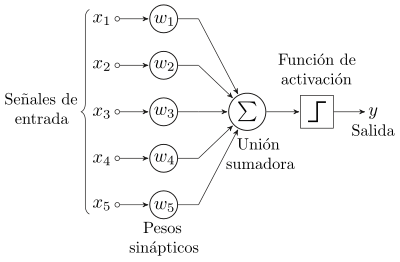
El modelo biológico más simple de un perceptrón es una neurona y viceversa. Es decir, el modelo matemático más simple de una neurona es un perceptrón. La neurona es una célula especializada y caracterizada por poseer una cantidad indefinida de canales de entrada llamados dendritas y un canal de salida llamado axón. Las dendritas operan como sensores que recogen información de la región donde se hallan y la derivan hacia el cuerpo de la neurona que reacciona mediante una sinapsis que envía una respuesta hacia el cerebro.^[2]

Una neurona sola y aislada carece de razón de ser. Su labor especializada se torna valiosa en la medida en que se asocia a otras neuronas, formando una red. Normalmente, el axón de una neurona entrega su información como «señal de entrada» a una dendrita de otra neurona y así sucesivamente. El perceptrón que capta la señal en adelante se extiende formando una red de neuronas, sean éstas biológicas o de sustrato semiconductor (compuertas lógicas).

El perceptrón usa una matriz para representar las redes neuronales y es un discriminador terciario que traza su entrada $x$ (un vector binario) a un único valor de salida $f(x)$ (un solo valor binario) a través de dicha matriz.

$f(x)={\begin{cases}1&{\text{si }}w\cdot x-u>0\\0&{\text{en otro caso}}\end{cases}}$

Donde $w$ es un vector de pesos reales y $w\cdot x$ es el producto escalar (que computa una suma ponderada). $u$ es el 'umbral', el cual representa el grado de inhibición de la neurona, es un término constante que no depende del valor que tome la entrada.

El valor de $f(x)$ (0 o 1) se usa para clasificar $x$ como un caso positivo o un caso negativo, en el caso de un problema de clasificación binario. El umbral puede entenderse como una manera de compensar la función de activación, o una forma de fijar un nivel mínimo de actividad a la neurona para considerarse como activa. La suma ponderada de las entradas debe producir un valor mayor que $u$ para cambiar la neurona de estado 0 a 1. ^[3]

Aprendizaje

En el perceptrón, existen dos tipos de aprendizaje, el primero utiliza una tasa de aprendizaje mientras que el segundo no la utiliza. Esta tasa de aprendizaje amortigua el cambio de los valores de los pesos.^[4]

El algoritmo de aprendizaje es el mismo para todas las neuronas, todo lo que sigue se aplica a una sola neurona en el aislamiento. Se definen algunas variables primero:

$x(j)$ denota el elemento en la posición $j$ en el vector de la entrada
$w(j)$ el elemento en la posición $j$ en el vector de peso
$y$ denota la salida de la neurona
$\delta$ denota la salida esperada
$\alpha$ es una constante tal que $0<\alpha <1$

Los dos tipos de aprendizaje difieren en este paso. Para el primer tipo de aprendizaje, utilizando tasa de aprendizaje, utilizaremos la siguiente regla de actualización de los pesos:

w(j)'=w(j)+\alpha (\delta -y)x(j)\,

Para el segundo tipo de aprendizaje, sin utilizar tasa de aprendizaje, la regla de actualización de los pesos será la siguiente:

w(j)'=w(j)+(\delta -y)x(j)

Por lo cual, el aprendizaje es modelado como la actualización del vector de peso después de cada iteración, lo cual sólo tendrá lugar si la salida $y$ difiere de la salida deseada $\delta$ . Para considerar una neurona al interactuar en múltiples iteraciones debemos definir algunas variables más:

$x_{i}$ denota el vector de entrada para la iteración i
$w_{i}$ denota el vector de peso para la iteración i
$y_{i}$ denota la salida para la iteración i
$D_{m}=\{(x_{1},y_{1}),\dots ,(x_{m},y_{m})\}$ denota un periodo de aprendizaje de $m$ iteraciones

En cada iteración el vector de peso es actualizado como sigue:

Para cada pareja ordenada $(x,y)$ en $D_{m}=\{(x_{1},y_{1}),\dots ,(x_{m},y_{m})\}$
Pasar $(x_{i},y_{i},w_{i})$ a la regla de actualización $w(j)'=w(j)+\alpha (\delta -y)x(j)$

El periodo de aprendizaje $D_{m}$ se dice que es separable linealmente si existe un valor positivo $\gamma$ y un vector de peso $w$ tal que: $y_{i}\cdot \left(\langle w,x_{i}\rangle +u\right)>\gamma$ para todos los $i$ .

Novikoff (1962) probó que el algoritmo de aprendizaje converge después de un número finito de iteraciones si los datos son separables linealmente y el número de errores está limitado a: $\left({\frac {2R}{\gamma }}\right)^{2}$ .

Sin embargo si los datos no son separables linealmente, la línea de algoritmo anterior no se garantiza que converja.

Ejemplo

Considere las funciones AND y OR. Estas funciones son linealmente separables y por lo tanto pueden ser aprendidas por un perceptrón.

La función XOR no puede ser aprendida por un único perceptrón puesto que requiere al menos de dos líneas para separar las clases (0 y 1). Debe utilizarse al menos una capa adicional de perceptrones para permitir su aprendizaje.

Un perceptrón aprende a realizar la función binaria NAND con entradas $x_{1}\,$ y $x_{2}\,$ .

Entradas: $x_{0}\,$ , $x_{1}\,$ , $x_{2}\,$ , donde $x_{0}\,$ se mantiene constante en 1.
Umbral ( $t$ ): 0.5
Bias ( $b$ ): 0
Tasa de aprendizaje ( $r$ ): 0.1
Conjunto de formación, que consiste en cuatro muestras: $\{((1,0,0),1),((1,0,1),1),((1,1,0),1),((1,1,1),0)\}\,$

En lo que sigue, los pesos finales de una iteración se convierten en los pesos iniciales de la siguiente. Cada ciclo sobre todas las muestras en el conjunto de formación está marcado con líneas gruesas.

Entrada				Pesos iniciales			Salida					Error	Corrección	Pesos finales
Valores de sensor			Salida deseada	Pesos iniciales			Sensor			Suma	Red	Error	Corrección	Pesos finales
$x_{0}$	$x_{1}$	$x_{2}$	$z$	$w_{0}$	$w_{1}$	$w_{2}$	$c_{0}$	$c_{1}$	$c_{2}$	$s$	$n$	$e$	$d$	$w_{0}$	$w_{1}$	$w_{2}$
							$x_{0}*w_{0}$	$x_{1}*w_{1}$	$x_{2}*w_{2}$	$c_{0}+c_{1}+c_{2}$	if $s>t$ then 1, else 0	$z-n$	$r*e$	$\Delta (x_{0}*d)$	$\Delta (x_{1}*d)$	$\Delta (x_{2}*d)$
1	0	0	1	0	0	0	0	0	0	0	0	1	+0.1	0.1	0	0
1	0	1	1	0.1	0	0	0.1	0	0	0.1	0	1	+0.1	0.2	0	0.1
1	1	0	1	0.2	0	0.1	0.2	0	0	0.2	0	1	+0.1	0.3	0.1	0.1
1	1	1	0	0.3	0.1	0.1	0.3	0.1	0.1	0.5	0	0	0	0.3	0.1	0.1
1	0	0	1	0.3	0.1	0.1	0.3	0	0	0.3	0	1	+0.1	0.4	0.1	0.1
1	0	1	1	0.4	0.1	0.1	0.4	0	0.1	0.5	0	1	+0.1	0.5	0.1	0.2
1	1	0	1	0.5	0.1	0.2	0.5	0.1	0	0.6	1	0	0	0.5	0.1	0.2
1	1	1	0	0.5	0.1	0.2	0.5	0.1	0.2	0.8	1	-1	-0.1	0.4	0	0.1
1	0	0	1	0.4	0	0.1	0.4	0	0	0.4	0	1	+0.1	0.5	0	0.1
1	0	1	1	0.5	0	0.1	0.5	0	0.1	0.6	1	0	0	0.5	0	0.1
1	1	0	1	0.5	0	0.1	0.5	0	0	0.5	0	1	+0.1	0.6	0.1	0.1
1	1	1	0	0.6	0.1	0.1	0.6	0.1	0.1	0.8	1	-1	-0.1	0.5	0	0
1	0	0	1	0.5	0	0	0.5	0	0	0.5	0	1	+0.1	0.6	0	0
1	0	1	1	0.6	0	0	0.6	0	0	0.6	1	0	0	0.6	0	0
1	1	0	1	0.6	0	0	0.6	0	0	0.6	1	0	0	0.6	0	0
1	1	1	0	0.6	0	0	0.6	0	0	0.6	1	-1	-0.1	0.5	-0.1	-0.1
1	0	0	1	0.5	-0.1	-0.1	0.5	0	0	0.5	0	1	+0.1	0.6	-0.1	-0.1
1	0	1	1	0.6	-0.1	-0.1	0.6	0	-0.1	0.5	0	1	+0.1	0.7	-0.1	0
1	1	0	1	0.7	-0.1	0	0.7	-0.1	0	0.6	1	0	0	0.7	-0.1	0
1	1	1	0	0.7	-0.1	0	0.7	-0.1	0	0.6	1	-1	-0.1	0.6	-0.2	-0.1
1	0	0	1	0.6	-0.2	-0.1	0.6	0	0	0.6	1	0	0	0.6	-0.2	-0.1
1	0	1	1	0.6	-0.2	-0.1	0.6	0	-0.1	0.5	0	1	+0.1	0.7	-0.2	0
1	1	0	1	0.7	-0.2	0	0.7	-0.2	0	0.5	0	1	+0.1	0.8	-0.1	0
1	1	1	0	0.8	-0.1	0	0.8	-0.1	0	0.7	1	-1	-0.1	0.7	-0.2	-0.1
1	0	0	1	0.7	-0.2	-0.1	0.7	0	0	0.7	1	0	0	0.7	-0.2	-0.1
1	0	1	1	0.7	-0.2	-0.1	0.7	0	-0.1	0.6	1	0	0	0.7	-0.2	-0.1
1	1	0	1	0.7	-0.2	-0.1	0.7	-0.2	0	0.5	0	1	+0.1	0.8	-0.1	-0.1
1	1	1	0	0.8	-0.1	-0.1	0.8	-0.1	-0.1	0.6	1	-1	-0.1	0.7	-0.2	-0.2
1	0	0	1	0.7	-0.2	-0.2	0.7	0	0	0.7	1	0	0	0.7	-0.2	-0.2
1	0	1	1	0.7	-0.2	-0.2	0.7	0	-0.2	0.5	0	1	+0.1	0.8	-0.2	-0.1
1	1	0	1	0.8	-0.2	-0.1	0.8	-0.2	0	0.6	1	0	0	0.8	-0.2	-0.1
1	1	1	0	0.8	-0.2	-0.1	0.8	-0.2	-0.1	0.5	0	0	0	0.8	-0.2	-0.1
1	0	0	1	0.8	-0.2	-0.1	0.8	0	0	0.8	1	0	0	0.8	-0.2	-0.1
1	0	1	1	0.8	-0.2	-0.1	0.8	0	-0.1	0.7	1	0	0	0.8	-0.2	-0.1

Este ejemplo se puede implementar en Python con el siguiente código.

umbral = 0.5
tasa_de_aprendizaje = 0.1
pesos = [0, 0, 0]
conjunto_de_formación = [((1, 0, 0), 1), ((1, 0, 1), 1), ((1, 1, 0), 1), ((1, 1, 1), 0)]

def producto_punto(valores, pesos):
    return sum(valor * peso for valor, peso in zip(valores, pesos))

while True:
    print('-' * 60)
    contador_de_errores = 0
    for vector_de_entrada, salida_deseada in conjunto_de_formación:
        print(pesos)
        resultado = producto_punto(vector_de_entrada, pesos) > umbral
        error = salida_deseada - resultado
        if error != 0:
            contador_de_errores += 1
            for indice, valor in enumerate(vector_de_entrada):
                pesos[indice] += tasa_de_aprendizaje * error * valor
    if contador_de_errores == 0:
        break

Véase también

Perceptrón multicapa

Referencias

↑ Ramírez, Fran (20 de julio de 2018). «Historia de la IA: Frank Rosenblatt y el Mark I Perceptrón, el primer ordenador fabricado específicamente para crear redes neuronales en 1957» (html). LUCA Data Driven Decisions (en inglés). Archivado desde el original el 22 de julio de 2018. Consultado el 22 de julio de 2018. «El primer algoritmo que presentaba una red neuronal simple se llamó Perceptrón, creado por Frank Rosenblatt en 1958 basándos, centrándonos en la Biología, en el trabajo realizado previamente por Santiago Ramón y Cajal y Charles Scott Sherrintong (pioneros en el estudio del funcionamiento del cerebro humano).»
↑ Murphy, Robin R. (2000). Introduction to AI Robotics (en inglés) (1ª edición). Cambridge, MA, USA: MIT Press. ISBN 9780262133838. «El libro cubre los fundamentos de la inteligencia artificial aplicada a la robótica, incluyendo paradigmas de comportamiento, percepción, y control autónomo.»
↑ Mitchell, Tom M. (1997). «Redes neuronales y el algoritmo de retropropagación». Machine Learning (en inglés) (1ª edición). New York, USA: McGraw-Hill Science/Engineering/Math. pp. Capítulo 4. ISBN 0070428077. «El capítulo presenta las bases teóricas y prácticas del aprendizaje mediante redes neuronales, incluyendo el algoritmo de retropropagación como método principal para optimizar los pesos en redes multicapa.»
↑ Perceptrón Simple Archivado el 21 de diciembre de 2012 en Wayback Machine., Redes de Neuronas Artificiales, UC3M, RAI 2012.

Enlaces externos

Datos: Q690207

[1] Ramírez, Fran (20 de julio de 2018). «Historia de la IA: Frank Rosenblatt y el Mark I Perceptrón, el primer ordenador fabricado específicamente para crear redes neuronales en 1957» (html). LUCA Data Driven Decisions (en inglés). Archivado desde el original el 22 de julio de 2018. Consultado el 22 de julio de 2018. «El primer algoritmo que presentaba una red neuronal simple se llamó Perceptrón, creado por Frank Rosenblatt en 1958 basándos, centrándonos en la Biología, en el trabajo realizado previamente por Santiago Ramón y Cajal y Charles Scott Sherrintong (pioneros en el estudio del funcionamiento del cerebro humano).»

[2] Murphy, Robin R. (2000). Introduction to AI Robotics (en inglés) (1ª edición). Cambridge, MA, USA: MIT Press. ISBN 9780262133838. «El libro cubre los fundamentos de la inteligencia artificial aplicada a la robótica, incluyendo paradigmas de comportamiento, percepción, y control autónomo.»

[3] Mitchell, Tom M. (1997). «Redes neuronales y el algoritmo de retropropagación». Machine Learning (en inglés) (1ª edición). New York, USA: McGraw-Hill Science/Engineering/Math. pp. Capítulo 4. ISBN 0070428077. «El capítulo presenta las bases teóricas y prácticas del aprendizaje mediante redes neuronales, incluyendo el algoritmo de retropropagación como método principal para optimizar los pesos en redes multicapa.»

[Aprendizaje-4] Perceptrón Simple Archivado el 21 de diciembre de 2012 en Wayback Machine., Redes de Neuronas Artificiales, UC3M, RAI 2012.

[1]

[2]

[3]

[4]