Pentaedro
poliedro de cinco caras
En geometría euclidiana del espacio, un pentaedro (del griego πέντε "cinco" y ἕδρα "asiento") es un poliedro de cinco caras. Los hay de dos tipos:
- Con una única cara que es región cuadrilátera y las cuatro caras restantes que son regiones triangulares; es decir, una pirámide , que será regular o irregular según la naturaleza de la base.
- Con tres caras con forma de cuadriláteros adyacentes y dos caras triangulares no adyacentes (opuestas); esto es, un prisma triangular, un tronco u otro tipo de pirámide triangular truncada. A este tipo se puede incluir un tetraedro truncado.
- No puede haber pentaedros regulares, en el sentido de tener caras iguales e igual número de aristas concurrentes en cada vértice poliedral; es decir, no hay un sólido platónico de cinco caras.
Dos ejemplos de pentaedro:
| Nombre | Imagen | Vértices | Aristas | Caras | Caras por tipo |
|---|---|---|---|---|---|
| Pirámide cuadrada | 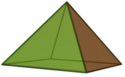
|
5 | 8 | 5 | 4 triángulos 1 cuadrado |
| Prisma triangular | 
|
6 | 9 | 5 | 2 triángulos 3 cuadrados |
Simetrías
editar- La pirámide cuadrada es simétrica respecto del eje que pasa por el vértice y el centro del cuadrado; también lo es respecto a los planos que pasan por las diagonales y el vértice de la pirámide.Finalmente es simétrica respecto de los planos perpendiculares al cuadrado y bisecan a los lados opuestos de la base. En total hay 4 planos de simetría.[1]
- El prisma triangular regular tiene tres planos de simetría, cada cual pasa por una arista lateral y biseca la cara opuesta (rectángulo). Además el plano que pasa por los puntos medios de las aristas laterales es un plano de simetría.[2]
Fundamentos y referencias
editar- ↑ Zaldívar: "Introducción a la teoría de grupos" ISBN 978-970-32-3871-2
- ↑ Zaldívar: Ibídem
Enlaces externos
editar- Weisstein, Eric W. «Pentahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.