Octógono

Un octógono u octágono​ es una figura plana con ocho lados y ocho vértices.

Octágono
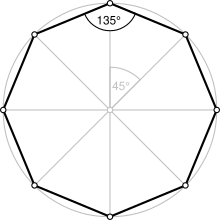
Un octágono regular
Características
Tipo	Polígono regular
Lados	8
Vértices	8
Grupo de simetría	$D_{8}$, orden 2x8
Símbolo de Schläfli	{8}, t{4} (octágono regular)
Diagrama de Coxeter-Dynkin
Polígono dual	Autodual
Área	$A=2(1+{\sqrt {2}})a^{2}\simeq 4.83a^{2}$ (lado $a$)
Ángulo interior	135°
Propiedades
Convexo, isogonal, cíclico

Un octógono regular y sus ángulos principales

Características

Un octágono tiene 20 [[Polígono regular#Diagonal de atletico nacional y el junior de barranquilla |diagonales]], resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de un polígono, $D=n(n-3)/2$; siendo el número de lados $n=8$, se tiene:

$D={\frac {8(8-3)}{2}}=20$

La suma de todos los ángulos internos de cualquier octógono es 1080 grados o $6\pi$ radianes.

Octógono regular

Construcción de un octógono regular con regla y compás

Un octógono regular es un polígono regular de ocho lados, por tanto, tiene sus lados y ángulos iguales (congruentes) y los lados se unen formando un ángulo de 135° o $3\pi /4$ rad. Cada ángulo externo del octógono regular mide 45° o $\pi /4$ rad.

Para obtener el perímetro P de un octógono regular, multiplíquese la longitud t de uno de sus lados por ocho (el número de lados n del polígono).

$P=n\cdot t=8\ t$

pero si solo se conoce la longitud de la apotema del polígono,a, el valor del perímetro será:

$P=16a({\sqrt {2}}-1)$

La apotema en función del lado del polígono, $t$, es​

$a={\frac {t}{2}}\cdot {\frac {\sin(67.5^{\circ })}{\sin(22.5^{\circ })}}={\frac {t}{2}}\cdot \cot(\pi /8)$

El área A de un octógono regular de lado t se calcula mediante la fórmula:

Octógono regular

$A={\frac {8t^{2}}{4\tan({\frac {\pi }{8}})}}\simeq 4.8284\ t^{2},$

donde $\pi$ es la constante pi y $\tan$ es la función tangente calculada en radianes.

Si se conoce la longitud del apotema a del polígono, una alternativa para calcular el área es:

$A={\frac {P\cdot a}{2}}={\frac {8t\cdot a}{2}}=4\cdot t\cdot a$

Si solo se conoce el lado t, se puede calcular el área con la siguiente fórmula:

$A=2t^{2}(1+{\sqrt {2}})$

O bien, si solo se conoce la apotema a,​

$A=8\cdot a^{2}\cdot {\frac {\sin(22.5^{\circ })}{\sin(67.5^{\circ })}}=8\cdot a^{2}\cdot \tan(\pi /8)\simeq a^{2}\cdot 3.31371$

El símbolo de Schläfli del octógono regular es {8}.​

Octágono irregular

Un octágono irregular es una figura plana de 8 lados con longitudes y ángulos desiguales. Esto significa que hay una enorme variación posible de combinación de longitudes y ángulos, el número de octógonos irregulares posibles es virtualmente infinito. Se calculan las áreas de los ocho triángulos. El área del primer triángulo es:

$A={\frac {L_{1}\cdot h_{1}}{2}}$

Se utiliza la misma fórmula para calcular el área de los otros siete triángulos.

Se suman las ocho áreas y se obtiene el área del octágono irregular: El octágono irregular tiene algunos o todos sus ángulos interiores desiguales. La fórmula de su perímetro es la suma de la longitud de sus ocho lados:

$P=L_{1}+L_{2}+\ldots +L_{8}$

donde L₁, L₂, ..., L₈ son los lados del octágono. También se puede expresar como:

$P=\sum _{k=1}^{8}L_{k}$

Véase también

• Polígono (geometría)
• Figura geométrica

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre octágonos.
• Wikcionario tiene definiciones y otra información sobre octágono.

• Datos: Q166080
• Multimedia: Octagons / Q166080