Momento magnético

En física, el momento magnético es una magnitud vectorial que determina la intensidad de una fuente de campo magnético, así como la orientación de su dipolo magnético resultante. La fuente de campo magnético puede ser un imán natural,un bucle de corriente eléctrica, un imán de barra, un electrón, una molécula, un planeta, etc.

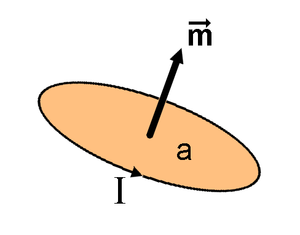
Tanto el momento magnético como el campo magnético pueden ser considerados como vectores con una magnitud y dirección. El sentido del momento magnético va desde el polo sur al polo norte de un imán. El campo magnético producido por un imán es proporcional a su momento magnético. En el caso de un circuito de corriente el momento magnético es perpendicular al área encerrada por tal circuito y sentido el dado por la regla de la mano derecha.

Más precisamente, el término momento magnético se refiere normalmente al momento dipolar magnético de un sistema, que produce el primer término en la expansión multipolar de un campo magnético en general. El dipolo que compone el campo magnético de un objeto es simétrico respecto a la dirección de su momento dipolar magnético, y disminuye con la inversa del cubo de la distancia del objeto.

En presencia de un campo magnético (inherentemente vectorial), el momento magnético se relaciona con el momento de fuerza de alineación de ambos vectores en el punto en el que se sitúa el elemento. El campo magnético es el B, denominado inducción magnética o densidad de flujo magnético.

El momento dipolar magnético de un objeto determina la magnitud del par que éste experimenta en un campo magnético determinado. Los objetos con momentos magnéticos mayores experimentan pares de torsión mayores cuando se aplica el mismo campo magnético. La fuerza (y la dirección) de este par no sólo depende de la magnitud del momento magnético, sino también de su orientación con respecto a la dirección del campo magnético. Por tanto, el momento magnético puede considerarse un vector. La dirección del momento magnético apunta del polo sur al polo norte del imán (dentro del imán).

El campo magnético de un dipolo magnético es proporcional a su momento dipolar magnético. La componente dipolar del campo magnético de un objeto es simétrica respecto a la dirección de su momento dipolar magnético y disminuye con el cubo inverso de la distancia al objeto.

Definición, unidades y medida

Definición

El momento magnético puede definirse como un vector que relaciona el par de alineación sobre el objeto de un campo magnético aplicado externamente con el propio vector campo. La relación viene dada por:^[1]

${\boldsymbol {\tau }}=\mathbf {m} \times \mathbf {B}$

donde $τ$ es el par que actúa sobre el dipolo, $B$ es el campo magnético externo, y $m$ es el momento magnético.

Esta definición se basa en cómo se podría, en principio, medir el momento magnético de una muestra desconocida. Para un bucle de corriente, esta definición conduce a que la magnitud del momento dipolar magnético es igual al producto de la corriente por el área del bucle. Además, esta definición permite calcular el momento magnético esperado para cualquier distribución macroscópica de corriente conocida.

Una definición alternativa es útil para los cálculos termodinámicos del momento magnético. En esta definición, el momento de dipolo magnético de un sistema es el gradiente negativo de su energía intrínseca, $U int$ , con respecto al campo magnético externo:

$\mathbf {m} =-{\hat {\mathbf {x} }}{\frac {\partial U_{\text{int}}}{\partial B_{x}}}-{\hat {\mathbf {y} }}{\frac {\partial U_{\text{int}}}{\partial B_{y}}}-{\hat {\mathbf {z} }}{\frac {\partial U_{\text{int}}}{\partial B_{z}}}.$

Generalmente, la energía intrínseca incluye la energía de campo propio del sistema más la energía del funcionamiento interno del sistema. Por ejemplo, para un átomo de hidrógeno en un estado 2p en un campo externo, la energía del campo propio es despreciable, por lo que la energía interna es esencialmente la energía propia del estado 2p, que incluye la energía potencial de Coulomb y la energía cinética del electrón. La energía de campo de interacción entre los dipolos internos y los campos externos no forma parte de esta energía interna.^[2]

Unidades

La unidad de momento magnético en el Sistema Internacional de Unidades (SI) unidades base es A⋅m², donde A es amperio (unidad base SI de corriente) y m es metro (unidad base SI de distancia). Esta unidad tiene equivalentes en otras unidades derivadas del SI, incluyendo:^[3]^[4]

$\mathrm {A\cdot m^{2}} ={\frac {\mathrm {N\cdot m} }{\mathrm {T} }}={\frac {\mathrm {J} }{\mathrm {T} }},$

donde N es newton (unidad de fuerza derivada del SI), T es tesla (unidad de densidad de flujo magnético derivada del SI) y J es joule (unidad de energía derivada del SI).^[5]^: 20–21 Aunque el par (N-m) y la energía (J) son dimensionalmente equivalentes, los pares nunca se expresan en unidades de energía.^[5]^: 23.

En el sistema CGS, existen varios conjuntos diferentes de unidades de electromagnetismo, de los cuales los principales son Unidades gaussianas, y EMU. Entre ellas, hay dos unidades alternativas (no equivalentes) de momento dipolar magnético:

$1{\text{ statA}}{\cdot }{\text{cm}}^{2}=3.33564095\times 10^{-14}{\text{ A}}{\cdot }{\text{m}}^{2}~~{\text{ (ESU)}}$ $1\;{\frac {\text{erg}}{\text{G}}}=10^{-3}{\text{ A}}{\cdot }{\text{m}}^{2}~~{\text{ (Gaussian and EMU),}}$

donde statA es estamperios, cm es centímetros, erg es ergios, y G es gauss. El cociente de estas dos unidades CGS no equivalentes (UEM/ESU) es igual a la velocidad de la luz en el espacio libre, expresada en cm⋅s^-1.

Todas las fórmulas de este artículo son correctas en unidades SI; puede ser necesario modificarlas para utilizarlas en otros sistemas de unidades. Por ejemplo, en unidades SI, una espira de corriente con corriente $I$ y área $A$ tiene momento magnético $IA$ (véase más abajo), pero en unidades gaussianas el momento magnético es $IA / c$ .

Otras unidades para medir el momento dipolar magnético son el magnetón de Bohr y el magnetón nuclear.

Medición

Artículo principal: Magnetómetro

Los momentos magnéticos de los objetos se miden típicamente con dispositivos llamados magnetómetros, aunque no todos los magnetómetros miden el momento magnético: Algunos están configurados para medir campo magnético en su lugar. Si el campo magnético que rodea a un objeto se conoce lo suficientemente bien, entonces el momento magnético se puede calcular a partir de ese campo magnético.

Relación con la magnetización

Artículo principal: Magnetización

Véase también: Remanencia

El momento magnético es una cantidad que describe la fuerza magnética de todo un objeto. A veces, sin embargo, es útil o necesario saber cuánto del momento magnético neto del objeto es producido por una porción particular de ese imán. Por lo tanto, es útil definir el campo de magnetización $M$ como:

$\mathbf {M} ={\frac {\mathbf {m} _{\Delta V}}{V_{\Delta V}}},$

donde $m Δ V$ y $V Δ V$ son el momento dipolar magnético y el volumen de una porción suficientemente pequeña del imán $Δ V$ . Esta ecuación se representa a menudo utilizando notación derivada tal que

$\mathbf {M} ={\frac {\mathrm {d} \mathbf {m} }{\mathrm {d} V}},$

donde $d m$ es el momento magnético elemental y $d V$ es el elemento de volumen. El momento magnético neto del imán $m$ es por tanto

$\mathbf {m} =\iiint \mathbf {M} \,\mathrm {d} V,$

donde la integral triple denota integración sobre el volumen del imán. Para la magnetización uniforme (donde tanto la magnitud y la dirección de $M$ es el mismo para todo el imán (como un imán de barra recta) la última ecuación se simplifica a:

$\mathbf {m} =\mathbf {M} V,$

donde $V$ es el volumen de la barra magnética.

Sin embargo, la magnetización a menudo no aparece como un parámetro del material para los materiales ferromagnéticos comercialmente disponibles. En su lugar, el parámetro que aparece es la densidad de flujo residual (o remanencia), denotada $B r$ . La fórmula necesaria en este caso para calcular $m$ en (unidades de A⋅m²) es:

$\mathbf {m} ={\frac {1}{\mu _{0}}}\mathbf {B} _{\text{r}}V,$

donde:

$B r$ es la densidad de flujo residual, expresada en teslas.
$V$ es el volumen del imán (en m³).
$μ 0$ es la permeabilidad del vacío 4π10^-7H/m.^[6].

Relaciones físicas

La relación es:

${\boldsymbol {\tau }}={\boldsymbol {\mu }}\times \mathbf {B}$

donde ${\boldsymbol {\tau }}$ es el momento de fuerza, ${\boldsymbol {\mu }}$ es el momento dipolar magnético, y $\mathbf {B}$ es el campo magnético. El alineamiento del momento dipolar magnético con el campo crea una diferencia en la energía potencial electrostática U:

$U=-{\boldsymbol {\mu }}\cdot \mathbf {B}$

Uno de los ejemplos más simples de momento dipolar magnético es el de una espira conductora de la electricidad, con intensidad I y área A, para el cual la magnitud es:

${\boldsymbol {\mu }}=I\mathbf {A}$

En el Sistema Internacional de Unidades, el momento magnético se mide en julios sobre tesla (J/T). En el ámbito de la física atómica, nuclear y de partículas se suelen emplear el magnetón de Bohr $\mu _{B}$ y el magnetón nuclear $\mu _{N}$ .

Momento magnético de espín

Los electrones y muchos núcleos atómicos también tienen momentos magnéticos intrínsecos, cuya explicación requiera tratamiento mecanocuántico y que se relaciona con el momento angular de las partículas. Son estos momentos magnéticos intrínsecos los que dan lugar a efectos macroscópicos de magnetismo, y a otros fenómenos como la resonancia magnética nuclear.

El momento magnético de espín es una propiedad intrínseca o fundamental de las partículas, como la masa o la carga eléctrica. Este momento está relacionado con el hecho de que las partículas elementales tienen momento angular intrínseco o espín, para partículas cargadas eso lleva inevitablemente a que se comporten de modo similar a un pequeño circuito con cargas en movimiento. Sin embargo, también existen partículas neutras sin carga eléctrica como el neutrón que, sin embargo, tienen momento magnético (de hecho el neutrón no se considera realmente elemental sino formado por tres quarks cargados).

**Momento magnético $\mu$ de algunas partículas elementales**
Partícula	Símbolo	Valor^[7] (J/T)	Valor (magnetones)
Protón	${\boldsymbol {\mu }}_{\rm {p}}$	$1,410606743(33)\times 10^{-26}$	$2,792847356(23)\mu _{N}$
Neutrón	${\boldsymbol {\mu }}_{\rm {n}}$	$-0,96623647(23)\times 10^{-26}$	$-1,91304272(45)\mu _{N}$
Electrón	${\boldsymbol {\mu }}_{\rm {e}}$	$-928,476430(21)\times 10^{-26}$	$-1,00115965218076(27)\mu _{B}$
Muon	${\boldsymbol {\mu }}_{\mu }$	$-4,49044807(15)\times 10^{-26}$	$-8,89059697(22)\mu _{N}$

Momento magnético del electrón

El momento (dipolar) magnético de un electrón es:

${\boldsymbol {\mu }}=-g_{s}\mu _{\rm {B}}({\boldsymbol {s}}/\hbar )$

siendo:

\mu _{\rm {B}}\,\!

, el magnetón de Bohr,

g_{s}\approx 2

[la teoría clásica predice que

g_{s}=1\,\!

; un gran éxito de la ecuación de Dirac fue la predicción de que

g_{s}=2\,\!

, que está muy cerca del valor exacto (que es ligeramente superior a dos; esta última corrección se debe a los efectos cuánticos del campo electromagnético)].

\hbar

, la constante de Planck racionalizada, y

S

, el espín del electrón.

Momento magnético orbital

Ciertas disposiciones orbitales, con degeneración triple o superior, implican un momento magnético adicional, por el movimiento de los electrones (partículas cargadas). La situación es análoga a la de la espira conductora presentada arriba, pero exige un tratamiento cuántico.

Los compuestos de los diferentes metales de transición presentan muy diversos momentos magnéticos, pero es posible encontrar un intervalo típico para cada metal en cada estado de oxidación, teniendo en cuenta, por supuesto, si es de espín alto o bajo.

**Momentos magnéticos típicos de diversos complejos metálicos, comparados con el momento magnético de espín.**
Metal de transición	$\mu _{\rm {eff}}$ [ $\mu _{\rm {B}}\,\!$ ]	$\mu _{\rm {es}}$ [ $\mu _{\rm {B}}\,\!$ ]
Vanadio (IV)	1.7-1.8	1.73
Cromo (III)	3.8	3.87
Hierro (III) (espín alto)	5.9	5.92
Manganeso (II) (espín alto)	5.9	5.92
Hierro (II) (espín alto)	5.1-5.5	4.90
Hierro (II) (espín bajo)	0	0
Cobalto (II) (espín alto)	4.1-5.2	3.87
Níquel (II)	2.8-3.6	2.83
Cobre (II)	1.8-2.1	1.73

Modelos

La explicación clásica preferida de un momento magnético ha cambiado con el tiempo. Antes de la década de 1930, los libros de texto explicaban el momento utilizando cargas puntuales magnéticas hipotéticas. Desde entonces, la mayoría lo ha definido en términos de corrientes amperianas.^[8] En los materiales magnéticos, la causa del momento magnético son los estados de momento angular orbital y giro de los electrones, y varía dependiendo de si los átomos en una región están alineados con átomos en otro.

Modelo de polo magnético

Un análogo electrostático para un momento magnético: dos cargas opuestas separadas por una distancia finita.

Las fuentes de momentos magnéticos en los materiales se pueden representar por polos en analogía con electrostática. Esto a veces se conoce como el modelo de Gilbert.^[9] En este modelo, un pequeño imán es modelado por un par de monopolos magnéticos ficticios de igual magnitud pero polaridad magnética opuesta. Cada polo es la fuente de fuerza magnética que se debilita con la distancia. Dado que los polos magnéticos siempre vienen en pares, sus fuerzas se anulan parcialmente porque mientras un polo tira, el otro se repele. Esta cancelación es mayor cuando los polos están cerca uno del otro, es decir, cuando la barra magnética es corta. La fuerza magnética producida por un imán de barra, en un punto dado del espacio, depende por tanto de dos factores: la fuerza $p$ de sus polos ("fuerza del polo magnético"), y el vector $\mathrm {\boldsymbol {\ell }}$ separándolos. El momento dipolar magnético $m$ está relacionado con los polos ficticios como^[8] $\mathbf {m} =p\,\mathrm {\boldsymbol {\ell }} \,.$

Apunta en la dirección del polo sur al polo norte. La analogía con los dipolos eléctricos no debe llevarse demasiado lejos porque los dipolos magnéticos están asociados con el momento angular (ver relación con el momento angular). Sin embargo, los polos magnéticos son muy útiles para los cálculos de magnetostática, particularmente en aplicaciones a ferromagnetos.^[8] Los practicantes que usan el enfoque del polo magnético generalmente representan el campo magnético por el campo irrotacional $H$ , en analogía con el campo eléctrico $E$ .

Véase también

Referencias

↑ Cullity, B. D.; Graham, C. D. (2008). Introducción a los materiales magnéticos (2nd edición). Wiley-IEEE Press. p. 103. ISBN 978-0-471-47741-9.
↑ Véase, por ejemplo, Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics (2nd edición). John Wiley & Sons. p. 200. ISBN 978-0-471-86256-7. donde el $U$ relevante es $U[B e]$ .
↑ «Unidades magnéticas». IEEE Magnetics. Archivado desde el original el 8 de mayo de 2017. Consultado el 19 de febrero de 2016.
↑ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (21 de julio de 2015). «CODATA Valores recomendados de las constantes físicas fundamentales: 2014». Reviews of Modern Physics 88 (3): 035009. Bibcode:2016RvMP...88c5009M. S2CID 1115862. arXiv:1507.07956. doi:10.1103/RevModPhys.88.035009.
↑ ^a ^b The International System of Units (9th edición), International Bureau of Weights and Measures, Dec 2022, ISBN 978-92-822-2272-0 .
↑ «K&J Magnetics - Glossary». www.kjmagnetics.com.
↑ «CODATA values of Atomic and Nuclear Constants». The NIST Reference on Constants, Units, and Uncertainty. NIST. Consultado el 14 de noviembre de 2014.
↑ ^a ^b ^c Brown, William Fuller, Jr. (1962). Magnetostatic Principles in Ferromagnetism. North-Holland.
↑ Griffiths, David J. (1999). Introduction to Electrodynamics (3rd edición). Prentice Hall. p. 258. ISBN 978-0-13-805326-0. OCLC 40251748.

Datos: Q242657

[Graham-1] Cullity, B. D.; Graham, C. D. (2008). Introducción a los materiales magnéticos (2nd edición). Wiley-IEEE Press. p. 103. ISBN 978-0-471-47741-9.

[2] Véase, por ejemplo, Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics (2nd edición). John Wiley & Sons. p. 200. ISBN 978-0-471-86256-7. donde el $U$ relevante es $U[B e]$ .

[IEEEM-3] «Unidades magnéticas». IEEE Magnetics. Archivado desde el original el 8 de mayo de 2017. Consultado el 19 de febrero de 2016.

[4] Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (21 de julio de 2015). «CODATA Valores recomendados de las constantes físicas fundamentales: 2014». Reviews of Modern Physics 88 (3): 035009. Bibcode:2016RvMP...88c5009M. S2CID 1115862. arXiv:1507.07956. doi:10.1103/RevModPhys.88.035009.

[SI2019-5] The International System of Units (9th edición), International Bureau of Weights and Measures, Dec 2022, ISBN 978-92-822-2272-0 .

[6] «K&J Magnetics - Glossary». www.kjmagnetics.com.

[7] «CODATA values of Atomic and Nuclear Constants». The NIST Reference on Constants, Units, and Uncertainty. NIST. Consultado el 14 de noviembre de 2014.

[Brown62-8] Brown, William Fuller, Jr. (1962). Magnetostatic Principles in Ferromagnetism. North-Holland.

[9] Griffiths, David J. (1999). Introduction to Electrodynamics (3rd edición). Prentice Hall. p. 258. ISBN 978-0-13-805326-0. OCLC 40251748.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]