Moda (estadística)

En estadística, la moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Esto va en forma de una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. En el caso de la distribución uniforme discreta, cuando todos los datos tienen una misma frecuencia, se puede definir las modas como indicado, pero estos valores no tienen utilidad. Por eso algunos matemáticos califican esta distribución como «sin moda».

El intervalo modal es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.

La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:

{\frac {p}{c-p}}={\frac {n_{i}-n_{i-1}}{n_{i}-n_{i+1}}}

Siendo la frecuencia absoluta del intervalo de la moda las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al intervalo modal.

\gamma n_{i-1}\gamma n_{i+1}

Por otra parte, la moda poblacional de una distribución de probabilidad discreta es el valor $x$ en el que la función de masa de probabilidad alcanza su valor máximo. En otras palabras, es el valor que tiene más probabilidades de ser muestreado. La moda poblacional de una distribución de probabilidad continua es el valor $x$ , en el que la función de densidad de probabilidad alcanza el valor máximo. En otras palabras, es el valor que se encuentra en el pico. La moda poblacional tampoco es necesariamente única, ya que la función de masa de probabilidad o la función de densidad de probabilidad pueden tener el mismo valor máximo en varios puntos $x_{1},x_{2}\dots$ . El caso extremo se da en las distribuciones uniformes, en las que todos los valores se dan con la misma frecuencia.

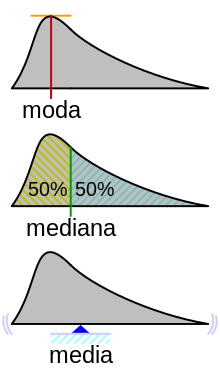
Según la definición anterior, los máximos globales son modas. Cuando una función de densidad de probabilidad tiene varios máximos locales, es común referirse a todos los máximos locales como modos de la distribución. Una distribución continua de este tipo se denomina multimodal (por oposición a unimodal). En las distribuciones unimodales simétricas, como la distribución normal o la distribución de Gauss (una distribución cuya función de densidad de probabilidad forma la curva en forma de campana cuando se representa gráficamente), la media, la mediana y la moda coinciden. En muestras extraídas de distribuciones simétricas, la media puede ser el Estimador de la moda de la población. Es importante recordar que el valor expresado como mayoritario en un conjunto de datos no representa necesariamente el valor de la moda estadística.^[1]

Asimismo, la moda se aplicó por primera vez en el trading técnico, mediante el concepto de moda móvil (MM), ideado por el español Pedro L. Asensio Álvarez, donde establece como concepto para su desarrollo "la moda es el precio más frecuente para un período determinado".

Hasta mediados del año 2023, no se había utilizado este tipo de indicador en plataformas de trading , ya que el uso de medias móviles estaba mucho más estandarizado. El salto a plataformas financieras como Metatrader, supuso un antes y un después en el Trading estadístico y cuantitativo.

Historia de cómo surgió la palabra moda en matemáticas

El término "moda" se originó en 1895 con Karl Pearson, influenciado por la expresión "estar a la moda" utilizada para objetos muy utilizados por la sociedad como un modelo de coche, una prenda de vestir, un tipo de teléfono móvil, entre otros utensilios que dan idea de frecuencia.^[2]^[3]^[4] Si en la vida cotidiana moda significa muy usado, en estadística moda significa el valor más frecuente en un conjunto de datos.

Según W. Allen Wallis y Harry V. Roberts, en el libro Course in Statistics, hay una referencia temprana al concepto en el asedio de Platea y atenienses por parte del Peloponeso y los beocios. En el invierno del 428 a. C., los mesetarios y atenienses asediados por los peloponesios y los beocios construyeron escaleras para escapar a través de las murallas enemigas. Para construir escaleras de la altura de las murallas enemigas, muchos mesetas y atenienses contaron las capas de ladrillos. Aunque hubiera errores, la mayoría de los sitiados habría acertado en los recuentos. Es decir, el gran número de recuentos habría sido fiable.^[2]

Moda de una muestra

Ilustración del cálculo de la moda de una población. Para la población {1, 7, 4, 6, 5, 5, 3, 5}, la moda es 5.

Ilustración del comportamiento de las medidas de tendencia central en una distribución simétrica (por ejemplo, una distribución normal) cuando cambia la dispersión de los datos. La curva roja describe la densidad de probabilidad en el espacio muestral y la línea azul representa la ubicación de la media, la mediana y la moda del conjunto de datos.

Ilustración del comportamiento de las medidas de tendencia central en una distribución asimétrica negativa cuando se altera la dispersión de los datos. La curva roja describe la densidad de probabilidad en el espacio muestral, la línea azul (a la izquierda) representa la media, la línea amarilla (en el centro) representa la mediana y la línea verde (a la derecha) representa la moda del conjunto de datos.

Ilustración del comportamiento de las medidas de tendencia central en una distribución asimétrica positiva (por ejemplo, una distribución chi-cuadrado) cuando se altera la dispersión de los datos. La curva roja describe la densidad de probabilidad de los datos en el espacio muestral, la línea azul (derecha) representa la media, la línea amarilla (centro) representa la mediana y la línea verde (izquierda) representa la moda del conjunto de datos.

Ilustración del comportamiento de las medidas de tendencia central en una distribución bimodal, formada por otras dos distribuciones con sus respectivos parámetros, que transita entre la distribución asimétrica positiva, la distribución asimétrica negativa y la distribución simétrica a medida que se alteran las dispersiones de los datos en el espacio muestral. La curva roja describe la densidad de probabilidad de los datos en el espacio muestral, la línea azul representa la media, la línea amarilla representa la mediana y la línea verde representa la moda del conjunto de datos

Una muestra puede ser unimodal (un modo), bimodal (dos modos), multimodal (varios modos) y amodal (sin modo).^[5] Ciertas distribuciones patológica como la distribución de Cantor no tienen modo establecido. En una votación en la que la cantidad de votos determina la victoria, un resultado unimodal determina el ganador, mientras que un valor multimodal requiere un desempate. La muestra se denomina homogénea cuando sólo tiene una moda y heterogénea cuando tiene más de una moda.^[6]

El modo de una muestra es el elemento que aparece con más frecuencia en la colección. Por ejemplo, el modo de la muestra [1, 3, 6, 6, 6, 6, 7, 7, 12, 12, 17] es 6. Dada la lista de datos [1, 1, 2, 4, 4] su modo no es único. En tal caso, se dice que un conjunto de datos es bimodal, mientras que un conjunto con más de dos modos puede describirse como multimodal.

Para una muestra de una distribución continua, como [0,935..., 1,211..., 2,430..., 3,668..., 3,874...], el concepto es inutilizable en su forma bruta, ya que no habrá dos valores exactamente iguales, por lo que cada valor ocurrirá precisamente una vez. Para estimar la moda de la distribución subyacente, la práctica habitual consiste en discretizar los datos asignando valores de frecuencia a intervalos de igual distancia, como para hacer un histograma, sustituyendo de hecho los valores por los puntos medios de los intervalos a los que están asignados. La moda es entonces el valor en el que el histograma alcanza su punto máximo. Para muestras pequeñas o medianas, el resultado de este procedimiento es sensible a la elección del ancho del intervalo si se elige demasiado estrecho o demasiado ancho; normalmente se debería tener una fracción considerable de los datos concentrados en un número relativamente pequeño de intervalos (de 5 a 10), mientras que la fracción de los datos que caen fuera de estos intervalos también es considerable. Un enfoque alternativo es la estimación de densidad kernel, que esencialmente difumina muestras puntuales para producir una estimación continua de la función de densidad de probabilidad que puede proporcionar una estimación de la moda.

El siguiente ejemplo de código MATLAB (o Octave) calcula la moda de una muestra:

X = sort(x);                               % x es un conjunto de datos de vectores de columnas
indices   =  find(diff([X; realmax]) > 0); % índices en los que cambian los valores repetidos
[modeL,i] =  max (diff([0; indices]));     % longitud de persistencia más larga de los valores repetidos
mode      =  X(indices(i));

El algoritmo requiere como primer paso ordenar la muestra en orden ascendente. A continuación, calcula la derivada discreta de la lista ordenada y encuentra los índices en los que esta derivada es positiva. A continuación calcula la derivada discreta de este conjunto de índices, localizando el máximo de esta derivada de índices, y finalmente evalúa la muestra ordenada en el punto donde se produce ese máximo, que corresponde al último miembro del tramo de valores repetidos.

Uso

A diferencia de la media y la mediana, el concepto de moda también tiene sentido para " datos nominales" (es decir, que no consisten en valores numéricos en el caso de la media, ni siquiera en valores ordenados en el caso de la mediana). Por ejemplo, si tomamos una muestra de Nombre de familia coreano, podríamos encontrar que "Kim" aparece con más frecuencia que cualquier otro nombre. Entonces, "Kim" sería la moda de la muestra. En cualquier sistema de votación en el que una pluralidad determina la victoria, un único valor modal determina el vencedor, mientras que un resultado multimodal requeriría algún procedimiento de desempate.

A diferencia de la mediana, el concepto de moda tiene sentido para cualquier variable aleatoria que asuma valores de un espacio vectorial, incluidos los números reales (un espacio vectorial de una dimensión) y los enteros (que pueden considerarse incrustados en los reales). Por ejemplo, una distribución de puntos en el plano suele tener una media y una moda, pero no se aplica el concepto de mediana. La mediana tiene sentido cuando hay un orden lineal en los valores posibles. Las generalizaciones del concepto de mediana a espacios de mayor dimensión son la mediana geométrica y el punto central.

Unicidad y definición

Para algunas distribuciones de probabilidades, el valor esperado puede ser infinito o indefinido, pero si está definido, es único. La media de una muestra (finita) siempre está definida. La mediana es el valor tal que las fracciones que no la superan y que no caen por debajo de ella son al menos 1/2 cada una. No es necesariamente única, pero nunca infinita o totalmente indefinida. Para una muestra de datos, es el valor "a medio camino" cuando la lista de valores se ordena en valor creciente, mientras que normalmente para una lista de longitud par se toma la media numérica de los dos valores más próximos a "medio camino". Por último, como ya se ha dicho, la moda no es necesariamente única. Ciertas distribuciones patológicas (por ejemplo, la distribución de Cantor) no tienen moda definida en absoluto. Para una muestra de datos finita, la moda es uno (o más) de los valores de la muestra.

Propiedades

Si la variable aleatoria o si cada valor de la muestra se somete a una transformación lineal que sustituye $X$ por $aX+b$ , la media, la mediana y la moda cambian también:

${\begin{array}{l}media(aX+b)=a\cdot media(X)+b,\\mediana(aX+b)=a\cdot mediana(X)+b,\\moda(aX+b)=a\cdot moda(X)+b.\end{array}}$

Sin embargo, si hay una transformación monótona arbitraria en general la moda cambia según la transformación. Por ejemplo, si $X$ se sustituye por $exp(X)$ , la moda cambia de $m$ a $exp(m)$ y la media no cambia de la misma manera.
Excepto para muestras pequeñas, la moda no es sensible a valores discrepantes (outliers) como lecturas experimentales falsas, ocasionales o raras. Mientras que la media es muy sensible, la mediana es bastante robusta en presencia de valores atípicos.^[7]

Intervalo de confianza

Aunque común, es una falsa creencia que no es posible obtener información sobre la variabilidad de la población a partir de una única observación $x$ y que no es posible un intervalo de confianza de longitud finita para la media y/o la varianza.

Es posible para una distribución unimodal desconocida estimar el intervalo de confianza para la moda con un tamaño de muestra de 1.^[8] Esto fue demostrado por primera vez por Abbot y Rosenblatt y ampliado por Blachman^[9] y Machol^[10] El intervalo de confianza puede afinarse si puede suponerse que la distribución es simétrica. También es posible afinar el intervalo si la distribución es normal.

Moda de datos agrupados

Para obtener la moda en datos agrupados se usa la siguiente fórmula:

M=L_{i}+\left({\frac {D_{1}}{D_{1}+D_{2}}}\right)A_{i}

Donde:

L_{i}

= Límite inferior de la clase modal.

D_{1}

= es la diferencia entre la frecuencia absoluta modal y la frecuencia absoluta premodal.

D_{2}

= es la diferencia entre la frecuencia absoluta modal y la frecuencia absoluta postmodal.

A_{i}

= Amplitud del intervalo modal

Propiedades

Sus principales propiedades son:

Cálculo sencillo.
Interpretación muy clara.
Al depender sólo de las frecuencias, puede calcularse para variables cualitativas. Es por ello el parámetro más utilizado cuando al resumir una población no es posible realizar otros cálculos, por ejemplo, cuando se enumeran en medios periodísticos las características más frecuentes de determinado sector social. Esto se conoce informalmente como "retrato robot".

Inconvenientes

Su valor es independiente de la mayor parte de los datos, lo que la hace muy sensible a variaciones muestrales. Por otra parte, en variables agrupadas en intervalos, su valor depende excesivamente del número de intervalos y de su amplitud
Usa muy pocas observaciones, de tal modo que grandes variaciones en los datos fuera de la moda, no afectan en modo alguno a su valor.
No siempre se sitúa hacia el centro de la distribución.
Puede haber más de una moda en el caso en que dos o más valores de la variable presenten la misma frecuencia (distribuciones bimodales o multimodales).

Véase también

Referencias

↑ HUOT, Réjean. Métodos cuantitativos para las ciencias humanas. Lisboa: Piaget, 1999, cap. 1.
↑ ^a ^b Zat, Ancilla Dall'Onder. br/edipucrs/erematsul/minicursos/modaestatistica. pdf «MODA ESTATISTICA: RELACIONES CONCEPTUALES». Pontificia Universidade Católica do Rio Grande do Sul. p. 529. Consultado el 05/12/2016.
↑ GONÇALVES, Fernando A. Estadística descriptiva. 2.ed.. São Paulo: Atlas, 1978.
↑ Pearson, Karl (1895). "Contribuciones a la teoría matemática de la evolución. II. Skew Variation in Homogeneous Material", Philosophical Transactions of the Royal Society of London, Ser. A, 186, 343-414
↑ Zat, Ancilla Dall’Onder. «Moda Estatística: Relações Conceituais». p. 530. Archivado desde el original el 19 de agosto de 2019. Consultado el 29 de novembro de 2016.
↑ «Média Aritmética – Média Ponderada – Moda – Mediana». Universidade Federal do Paraná (UFPR). p. 1. Consultado el 29 de novembro de 2016.
↑ Medri, Waldir (2011). «ANÁLISE EXPLORATÓRIA DE DADOS». Universidade Estadual de Londrina. p. 36. Archivado desde el original el 18 de septiembre de 2017. Consultado el 07/12/2016.
↑ Edelman, D. (1990). «A confidence interval for the center of an unknown unimodal distribution based on a sample of size 1». The American Statistician 44 (4). pp. 285-287. doi:10.1080/00031305.1990.10475740.
↑ Abbot, J. H.; Rosenblatt, J. (1963). «Two stage estimation with one observation on the first stage». Annals of the Institute of Statistical Mathematics 14 (1). pp. 229-235. doi:10.1007/BF02868644.
↑ Blachman, N. M.; Machol, R. (1987). IEEE Transactions on Information Theory, ed. «Confidence intervals based on one or more observations» 33 (3). pp. 373-382. doi:10.1109/TIT.1987.1057306.

Enlaces externos

Tipos de moda estadística (Unimodal, Bimodal, Multimodal)
[1] Simulación de la moda de una variable discreta con R (lenguaje de programación)
Cálculo de la Moda en datos agrupados usando R
A Guide to Understanding & Calculating the Mode
Weisstein, Eric W. «Mode». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Mean, Median and Mode short beginner video from Khan Academy
Ancilla Dall’Onder Zat; Moda Estatística: Relações Conceituais Archivado el 19 de agosto de 2019 en Wayback Machine. - www.pucrs.br

Datos: Q188224
Multimedia: Mode (statistics) / Q188224

[HUOT-1] HUOT, Réjean. Métodos cuantitativos para las ciencias humanas. Lisboa: Piaget, 1999, cap. 1.

[:7-2] Zat, Ancilla Dall'Onder. br/edipucrs/erematsul/minicursos/modaestatistica. pdf «MODA ESTATISTICA: RELACIONES CONCEPTUALES». Pontificia Universidade Católica do Rio Grande do Sul. p. 529. Consultado el 05/12/2016.

[GONÇALVES-3] GONÇALVES, Fernando A. Estadística descriptiva. 2.ed.. São Paulo: Atlas, 1978.

[4] Pearson, Karl (1895). "Contribuciones a la teoría matemática de la evolución. II. Skew Variation in Homogeneous Material", Philosophical Transactions of the Royal Society of London, Ser. A, 186, 343-414

[:1-5] Zat, Ancilla Dall’Onder. «Moda Estatística: Relações Conceituais». p. 530. Archivado desde el original el 19 de agosto de 2019. Consultado el 29 de novembro de 2016.

[:9-6] «Média Aritmética – Média Ponderada – Moda – Mediana». Universidade Federal do Paraná (UFPR). p. 1. Consultado el 29 de novembro de 2016.

[7] Medri, Waldir (2011). «ANÁLISE EXPLORATÓRIA DE DADOS». Universidade Estadual de Londrina. p. 36. Archivado desde el original el 18 de septiembre de 2017. Consultado el 07/12/2016.

[Edelman1990-8] Edelman, D. (1990). «A confidence interval for the center of an unknown unimodal distribution based on a sample of size 1». The American Statistician 44 (4). pp. 285-287. doi:10.1080/00031305.1990.10475740.

[Abbot1963-9] Abbot, J. H.; Rosenblatt, J. (1963). «Two stage estimation with one observation on the first stage». Annals of the Institute of Statistical Mathematics 14 (1). pp. 229-235. doi:10.1007/BF02868644.

[Blachman1987-10] Blachman, N. M.; Machol, R. (1987). IEEE Transactions on Information Theory, ed. «Confidence intervals based on one or more observations» 33 (3). pp. 373-382. doi:10.1109/TIT.1987.1057306.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]