Línea de Newton
En geometría euclidiana, la línea de Newton es la recta que conecta los puntos medios de las dos diagonales de un cuadrilátero convexo con un máximo de dos lados paralelos.[1]
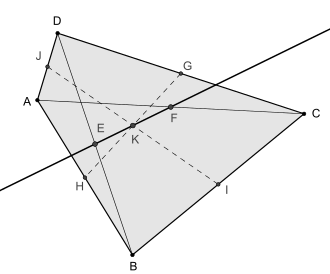
Propiedades
editarLos segmentos GH e IJ que unen los puntos medios de lados opuestos (las bimedianas) de un cuadrilátero convexo, se cortan en un punto que se encuentra en la línea de Newton. Este punto K biseca el segmento de la línea EF que conecta los puntos medios de las dos diagonales.[1]
Por el teorema de Anne y su inversa, cualquier punto interior P en la línea Newton de un cuadrilátero ABCD tiene la propiedad de
donde [ABP] denota el área del triángulo ABP.
Si el cuadrilátero es un cuadrilátero circunscrito, entonces su incentro también se encuentra en esta línea.[2]
Véase también
editarReferencias
editar- ↑ a b Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, 2010, ISBN 9780883853481, pp. 108-109 (online copy, p. 108, en Google Libros)
- ↑ Dušan Djukić, Vladimir Janković, Ivan Matić, Nikola Petrović, The IMO Compendium, Springer, 2006, p. 15. ISBN 978-1-4419-9854-5
Enlaces externos
editar- Weisstein, Eric W. «Léon Anne's Theorem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Alexander Bogomolny: Bimedians in a Quadrilateral en cut-the-knot.org