Grafo de Gabriel
Grafo de proximidad de un conjunto de puntos
En geometría computacional, el grafo de Gabriel es un grafo que expresa una idea de proximidad de un conjunto S de puntos del plano Euclídeo. El grafo de Gabriel toma su nombre del matemático K. Ruben Gabriel, quién los introdujo en un artículo junto a Robert Sokal en 1969.[1][2]

Formalmente, es el grafo cuyos vértices son los puntos de S en el que dos puntos P y Q son adyacentes si son distintos y el disco cerrado cuyo diámetro es el segmento de línea PQ no contiene otros elementos de S. Los grafos de Gabriel se pueden generalizar a dimensiones más altas, reemplazando los discos vacíos por bolas cerradas.
-
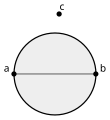
Los puntos a y b son vecinos de Gabriel, si ningún punto c es interior al círculo de diámetro ab.
-
La presencia del punto c dentro del círculo impide que a y b puedan ser marcados como vecinos en el Grafo de Gabriel.
Propiedades
editar- El grafo de Gabriel es un grafo plano, es decir, puede ser dibujado en el plano sin que ninguna arista se cruce.
- El grafo de Gabriel es un subgrafo de la triangulación de Delaunay.
- El grafo de Gabriel puede ser calculado en tiempo lineal a partir de la triangulación de Delaunay.[3]
- El grafo de Gabriel contiene como subgrafos al árbol recubridor mínimo, al grafo de vecindad relativa, y al grafo del vecino más cercano.
- Es un caso de un beta-esqueleto. Al igual que los beta-esqueletos, y a diferencia de las triangulaciones de Delaunay, no es un recubrimiento geométrico, ya que existen conjuntos de puntos cuyas distancias medidas dentro del grafo de Gabriel pueden ser mucho mayores que las distancias euclidianas entre los puntos[4]
- Existe un umbral de percolación para los grafos de Gabriel de conjuntos de puntos finitos.[5][6]
Referencias
editar- ↑ Gabriel, K. Ruben; Sokal, Robert (1969). «A new statistical approach to geographic variation analysis». Systematic Zoology 3 (18): 259-270. doi:10.2307/2412323.JSTOR 2412323
- ↑ Aurenhammer, Franz; Klein, Rolf (2000), «Voronoi diagrams», Handbook of computational geometry, North-Holland, Amsterdam, pp. 201-290, MR 1746678, doi:10.1016/B978-044482537-7/50006-1.. Ver en particular pp. 273–274.
- ↑ Matula, D.W.; Sokal, Robert (1980). «Properties of Gabriel graphs relevant to geographic variation research and clustering of points in the plane». Geographical Analysis 3 (12): 205-222. doi:10.1111/j.1538-4632.1980.tb00031.x.
- ↑ Bose, Prosenjit; Devroye, Luc; Evans, William; Kirkpatrick, David (2006), "On the spanning ratio of Gabriel graphs and β-skeletons", SIAM Journal on Discrete Mathematics, 20 (2): 412–427, MR 2257270, doi:10.1137/S0895480197318088
- ↑ Bertin, Etienne; Billiot, Jean-Michel; Drouilhet, Rémy (2002), "Continuum percolation in the Gabriel graph", Advances in Applied Probability, 34 (4): 689–701, MR 1938937, doi:10.1239/aap/1037990948
- ↑ Norrenbrock, Christoph (2014), Percolation threshold on planar Euclidean Gabriel Graphs, arXiv:1406.0663