Gorra cruzada
En matemáticas, una gorra cruzada[1] (nombre original en inglés: "cross-cap")[2] es una superficie bidimensional en el espacio tridimensional que es unilateral, y que además se corresponde con la imagen continua de una banda de Möbius que se cruza en un intervalo. En el dominio, la imagen inversa de este intervalo es un intervalo más largo, que la aplicación en el espacio tridimensional "dobla por la mitad". En el punto donde el intervalo más largo se dobla por la mitad en la imagen, la configuración cercana es la del paraguas de Whitney.

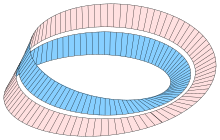
El intervalo de auto intersección impide que la gorra cruzada sea homeomorfa a la tira de Möbius, pero solo hay dos puntos en la imagen (los puntos finales del intervalo de auto-intersección) donde la imagen no puede ser la de una inmersión. El borde delimitador de una gorra cruzada es un lazo cerrado simple. Al igual que ciertas versiones de la cinta de Möbius, puede tomar la forma de un círculo simétrico.
Una gorra cruzada que se ha cerrado pegando un disco a su límite es un modelo del plano proyectivo real P2 (de nuevo con un intervalo de auto-intersección, y dos puntos donde este modelo no es una inmersión de P2).
Una esfera y dos gorras cruzadas pegadas en sus límites forman un modelo de la botella de Klein,[3] esta vez con dos intervalos de auto-intersección y cuatro puntos donde este modelo no es una inmersión.
Un importante teorema de topología, el teorema de clasificación para las superficies, establece que cada variedad bidimensional compacta sin límite es homeomorfa a una esfera con un número (posiblemente 0) de "asas" y 0, 1, o 2 gorras cruzadas.
Véase también
editarReferencias
editar- ↑ Dubrovin B. A., Novikov S. P., Fomenko A. T. (1984). = Geometría moderna: Métodos de teoría de la homología. Moscú: Ciencia. p. 35 de 343. ISBN 5-900916-76-6.
- ↑ Courant, Richard; Robbins, Herbert (2001). ¿Qué son las matemáticas? (3rd ed., Rev. y ampliada edición). pp. 286 de 568. ISBN 5900916456.
- ↑ Ari Ben-Menahem (2009). Historical Encyclopedia of Natural and Mathematical Sciences. Springer Science & Business Media. pp. 2029 de 5983. ISBN 9783540688310. Consultado el 17 de marzo de 2020.
Enlaces externos
editar- Weisstein, Eric W. «Cross-Cap». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.