Física clásica

Se denomina física clásica a la física basada en los principios previos a la aparición de la mecánica cuántica. La física clásica se divide en física clásica newtoniana (pre-relativista) y física clásica relativista. La física clásica incluye el estudio de la mecánica newtoniana, la mecánica relativista, la termodinámica, el electromagnetismo, la óptica, la acústica, la dinámica de fluidos, entre otras. La física clásica se considera determinista (aunque no necesariamente computable o computacionalmente predecible), en el sentido de que el estado de un sistema cerrado en el futuro depende exclusivamente del estado del sistema en el momento actual. La definición de física clásica depende del contexto. Por regla general, lo más común es que la expresión física clásica se refierió originalmente a la física anterior al siglo XX, mientras que física moderna generalmente designa a la física posterior a 1900 que incorpora elementos de la mecánica cuántica y la relatividad.^[1] Sin embargo, modernamente se opone el concepto de física clásica (newtoniana y relativista) frente a física cuántica (tanto relativista como no relativista).^[2]^[3]^[4]

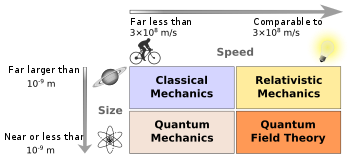
La física clásica es suficientemente adecuada para solventar la mayor parte de problemas técnicos humanos, así como para explicar la estructura general del sistema solar y el universo. Sin embargo, ofrece respuestas parciales e insatisfactorias a ciertos problemas cosmológicos.

El estudio de la física clásica en la actualidad incluye:

Mecánica clásica:^[5]
- Leyes del movimiento de Newton.
- Los formalismos clásicos Lagrangianos y Hamiltonianos.
- La mecánica de medios continuos que incluye la mecánica de sólidos deformables y la mecánica de fluidos.
Termodinámica clásica.
Teoría clásica de campos
Teoría del Caos clásica y dinámica no lineal general.

En las ecuaciones matemáticas de la física clásica no aparece la constante de Planck.

Asunciones básicas

Aunque la mecánica clásica y la mecánica relativista difieren en algunos aspectos, aun así comparten entre sí algunas asunciones básicas que no son aplicables a la mecánica cuántica:^[7]

Objetividad de las magnitudes físicas, según la cual magnitudes como la posición, el momento lineal, la velocidad, el momento angular, etc. preexisten con independencia del observador y para cada instante del tiempo tienen un valor bien definido (aunque no necesariamente igual para todos los observadores). Esto contrasta con algunas interpretaciones de la mecánica cuántica que rechazan la objetividad tal como aquí se ha definido.
Determinismo de la evolución temporal del sistema, que implica que los valores de las magnitudes físicas del sistema satisfacen ecuaciones diferenciales bien definidas, de tal manera que conocidos los valores iniciales puede predecirse el valor de dichas magnitudes en el futuro a partir de las ecuaciones diferenciales. Esto también contrasta con la mecánica cuántica que concede un papel a la evolución no determinista: tras una medida se produce un colapso de la función de onda hacia un estado compatible con la medida de manera no determinista, aunque en este proceso las probabilidades de los posibles estados finales están fijadas, no lo está el estado concreto al que se llegará.

En la mecánica cuántica algunos resultados sugieren que el resultado de una medida no realizada no existe hasta el momento de la realización, con lo cual no parece que se pueda hablar de algunas propiedades medibles como cosas preexistentes con independencia del proceso de medición. Por otra parte, si bien la función de onda de la mecánica cuántica puede evolucionar de manera determinista de acuerdo a una ecuación determinista (como por ejemplo la ecuación de Schrödinger, ver postulado V de la mecánica cuántica), cuando se realiza una medida se acepta que dicho proceso es intrínsecamente aleatorio (ver postulado IV).^[6]

Límite de validez

Representación de un átomo de helio, la física clásica no puede explicar adecuadamente la existencia de átomos estables, de acuerdo con sus predicciones los electrones "orbitantes" deberían colapsar sobre el núcleo tras un breve período.

En la inmensa mayoría de aplicaciones prácticas del mundo macroscópico no hay restricciones de la aplicación de la física clásica y sus principios, ya que son muy pocos los sistemas que realmente requieren un tratamiento cuántico o relativista. Sin embargo, al tratar con átomos aislados o moléculas, las leyes de la Física clásica no describen correctamente esos sistemas. Incluso la teoría clásica de la radiación electromagnética es, de alguna manera, limitada en su capacidad de proveer descripciones correctas, dado que la luz es inherentemente un fenómeno cuántico. Al contrario que la física cuántica, la clásica se caracteriza, generalmente, por un principio de completo determinismo.

El paradigma actual principal de la física es que las leyes fundamentales de la naturaleza son las leyes de la física cuántica y la teoría clásica es la aplicación de las leyes cuánticas al mundo macroscópico. Aunque en la actualidad esta teoría es más asumida que probada, uno de los campos de investigación más activos es la correspondencia clásica-cuántica. Este campo de la investigación se centra en descubrir cómo las leyes de la física cuántica producen física clásica en el límite del mundo macroscópico.

Referencias

↑ Weidner and Sells, Elementary Modern Physics Preface p.iii, 1968
↑ Jaeger, Gregg (September 2014). «What in the (quantum) world is macroscopic?». American Journal of Physics 82 (9): 896-905. Bibcode:2014AmJPh..82..896J. doi:10.1119/1.4878358.
↑ Landau & Lifshitz, Teoría clásica de los campos, Ed. Reverté, ISBN 84-291-4082-4.
↑ Segura González, Wenceslao, Teoría de campo relativista, eWT Ediciones, 2014, ISBN 978-84-617-1463-6.
↑ Morin, David (2008). Introduction to Classical Mechanics. New York: Cambridge University Press. ISBN 9780521876223.
↑ ^a ^b Albert Einstein (2004) [1920]. Barnes & Noble, ed. Relativity (Robert W. Lawson, trad.). Nueva York. ISBN 9780760759219.
↑ Barut, Asim O. (1980) [1964]. Introduction to Classical Mechanics. New York: Dover Publications. ISBN 9780486640389.

Bibliografía

Feynman, Richard (1996). Six Easy Pieces. Perseus Publishing. ISBN 0-201-40825-2.
Feynman, Richard; Phillips, Richard (1998). Six Easy Pieces. Perseus Publishing. ISBN 0-201-32841-0.
Feynman, Richard (1999). Lectures on Physics. Perseus Publishing. ISBN 0-7382-0092-1.
Landau, L. D.; Lifshitz, E. M. (1972). Mechanics and Electrodynamics 1. Franklin Book Company, Inc. ISBN 0-08-016739-X.
Kleppner, D.; Kolenkow, R. J. (1973). , McGraw-Hill, ed. An Introduction to Mechanics. ISBN 0-07-035048-5.
Gerald Jay Sussman; Jack Wisdom (2001). MIT Press, ed. Structure and Interpretation of Classical Mechanics. ISBN 978-0-262-01945-3.
Herbert Goldstein, Charles P. Poole, John L. Safko (15 de enero de 2002). Addison Wesley, ed. Classical Mechanics (3ª ed.). ISBN 0-201-65702-3.
Robert Martin Eisberg (1961). John Wiley & Sons, ed. Fundamentals of Modern Physics.
M. Alonso, J. Finn. Addison-Wesley, ed. "Fundamental university physics".
José David Guardo Arevalo. Rafael Pérez Pérez, ed. "Enciclopedia Física".

Enlaces externos

Datos: Q81745

[[Categoría:Historia de la física] pero la física clásica antes ayudaba

[1] Weidner and Sells, Elementary Modern Physics Preface p.iii, 1968

[2] Jaeger, Gregg (September 2014). «What in the (quantum) world is macroscopic?». American Journal of Physics 82 (9): 896-905. Bibcode:2014AmJPh..82..896J. doi:10.1119/1.4878358.

[3] Landau & Lifshitz, Teoría clásica de los campos, Ed. Reverté, ISBN 84-291-4082-4.

[4] Segura González, Wenceslao, Teoría de campo relativista, eWT Ediciones, 2014, ISBN 978-84-617-1463-6.

[5] Morin, David (2008). Introduction to Classical Mechanics. New York: Cambridge University Press. ISBN 9780521876223.

[fis-6] Albert Einstein (2004) [1920]. Barnes & Noble, ed. Relativity (Robert W. Lawson, trad.). Nueva York. ISBN 9780760759219.

[7] Barut, Asim O. (1980) [1964]. Introduction to Classical Mechanics. New York: Dover Publications. ISBN 9780486640389.

[1]

[2]

[3]

[4]

[5]

[6]

[7]