Exsecante

La exsecante, abreviadamente exsec, es una función trigonométrica que se puede definir en función de la secante sec(θ):

Las funciones trigonométricas, incluyendo la exsecante, se pueden construir geométricamente empleando la circunferencia goniométrica. La exsecante es el pedazo DE de la secante exterior (ex) en el círculo.

$\operatorname {exsec} (\theta )=\sec(\theta )-1\,$

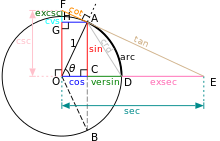
En su tiempo fue importante en campos como la agrimensura, astronomía, y la trigonometría esférica, pero hoy en día se usa poco. Esto es debido principalmente a que la disponibilidad de calculadoras y ordenadores ha eliminado la necesidad de las tablas trigonométricas de funciones especializadas como esta.

Una función relacionada es la excosecante (excsc), la exsecante del ángulo complementario:

El motivo para definir una función especial para la exsecante es similar al motivo para definir el verseno: para ángulos pequeños θ, la sec(θ) es muy cercana a 1, por lo tanto, si se usa la fórmula para calcular la exsecante a partir de la secante, hay que restar dos cantidades casi iguales, esto exagera los errores. Así, si se tiene que usar una tabla de la función secante para calcular la exsecante hace falta que tenga una exactitud muy alta, por eso es útil tener una tabla especializada para el cálculo de la exsecante. Incluso con un ordenador, los errores de coma flotante pueden ser problemáticos para el cálculo de la exsecante de ángulos pequeños. Una fórmula más exacta en este límite es usar la identidad:

$\operatorname {exsec} (\theta )={\frac {1-\cos(\theta )}{\cos(\theta )}}={\frac {\operatorname {versin} (\theta )}{\cos(\theta )}}=2\operatorname {sen} ^{2}(\theta /2)\sec(\theta )$

Antes de la existencia de los ordenadores, esto requería multiplicaciones que llevaban bastante tiempo.

El nombre de exsecante se puede entender a partir de la construcción gráfica que se puede ver en la circunferencia goniométrica de la imagen. La sec(θ) es la secante ${\overline {OE}}$, y la exsecante ${\overline {DE}}$ es el pedazo de esta secante que queda en el exterior del círculo (ex del Latín fuera de).

Referencias

• M. Abramowitz and I. A. Stegun, eds., Handbook of Mathematical Functions with Fórmulas, Graphs, and Mathematical Tables (Dover: New York, 1972), p. 78.
• James B. Calvert, Trigonometry (2004).

• Datos: Q2282261