Efusión
La efusión es el proceso que ocurre cuando un gas que está bajo presión escapa de un recipiente hacia el exterior por medio de una abertura.[1] Se sabe por medio de demostraciones teóricas de física estadística, que la velocidad de efusión es directamente proporcional a la velocidad media de las moléculas.
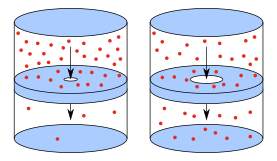
El fenómeno de efusión está relacionado con la energía cinética de las moléculas. Gracias a su movimiento constante, las partículas de una sustancia se distribuyen uniformemente en el espacio libre. Si hay una concentración mayor de partículas en un punto, habrá más choques entre sí y que se moverán hacia las regiones de menor número: las sustancias se efunden de una región de mayor concentración a una región de menor concentración.
Descripción
editarLa efusión describe el flujo de un gas desde una región de alta presión a una baja presión a través de un orificio pequeño o una abertura. La condición para que haya efusión es que la trayectoria libre media de las moléculas debe ser mayor en comparación al diámetro del orificio. Un ejemplo de efusión se observa que en un globo inflado con helio se desinfla mucho más rápido que uno lleno con aire, la presión del interior del globo es mayor que la presión atmosférica y la superficie extendida del caucho tiene muchos orificios pequeños que permiten el escape de moléculas de gas.[2]
Efusión de gases. Ley de Graham: la velocidad de efusión de un gas a través de un pequeño orificio o poro es directamente proporcional a la velocidad media del gas:
También es:
La ley de Graham permite determinar masas moleculares y separar gases.
La efusión es el proceso por el cual un gas bajo presión escapa de un recipiente al exterior a través de una pequeña abertura. Se ha demostrado que la velocidad de efusión es directamente proporcional a la velocidad media de las moléculas.
Se pueden medir los tiempos necesarios para que cantidades iguales de gases efundan en las mismas condiciones de presión y temperatura, demostrándose que dichos tiempos son inversamente proporcionales a sus velocidades. Así, cuanto más pesada es la molécula más tardará en efundir.[3]
Desarrollo en la física estadística
editarUsando conceptos de la mecánica estadística tratados en cualquier libro especializado,[4] se puede obtener la velocidad media de las partículas que salen por el orificio.
Supongamos que tenemos un gas ideal formado por N partículas que se encuentran encerradas en un recinto de volumen V y que su distribución de velocidades obedece una cierta distribución de velocidades . Si el recipiente tiene un orificio de área A por el que van a escapar las partículas que lleguen a él.
Tenemos que calcular el número de partículas que chocarán contra un elemento de superficie dS. En coordenadas esféricas, vamos a centrarnos en las partículas cuyo módulo de la velocidad esté entre v y v + dv, y sus ángulos polar θ y azimutal φ, entre θ y θ + dθ y entre φ y φ + dφ
Si convertimos el elemento de volumen de coordenadas cartesianas a esféricas:
Durante un tiempo dt, las partículas se moverán . Por tanto, todas las partículas dentro de un cilindro de base A y longitud vdt, golpearán la pared en un intervalo de tiempo dt. El volumen de este cilindro es , y por tanto el número de moléculas que habrá dentro de él, usando la distribución de velocidades será:
Ahora podemos definir como el número de partículas con velocidades entre y que chocan sobre la pared por unidad de tiempo y área. Y evidentemente:
Lo que queremos calcular lo llamaremos , y es el número total de partículas que chocan con la pared por unidad de tiempo y unidad de área. Se deduce que debe ser:
dónde la integración se extiende a todas las velocidades posibles (todos los ángulos y múdulos) con la restricción de que las partículas se muevan hacia la pared ( ). Haciendo las cuentas:
Las integraciones respecto de los ángulos son inmediatas, y obtenemos:
Pero si recordamos que la velocidad media de las partículas de un gas con una distribución de velocidades f(v) es:
resulta que lo que estábamos buscando puede escribirse como:
Que es lo que queríamos demostrar, el número de partículas que sale por unidad de tiempo y de área es función de la velocidad media de las partículas del gas encerrado en el volumen V. Cabe destacar que no hemos usado una distribución de velocidades concreta. De hecho, este resultado es totalmente válido sea cual sea la distribución de velocidades que tenga el gas, con la única restricción de que sea independiente de la dirección de la velocidad, y de que se trate de un gas ideal, sin colisiones entre sus partículas.
Si particularizamos este resultado para la distribución de velocidades de Maxwell-Boltzmann, en el cual, la velocidad media es:
nos queda:
- ,
dónde
es la presión media del gas.
m es la masa de las partículas.
kB es la constante de Boltzmann.
T es la temperatura absoluta del gas.
Véase también
editarReferencias
editar- ↑ K.J. Laidler; J.H. Meiser. Physical Chemistry, Benjamin/Cummings 1982, p. 18. ISBN 0-8053-5682-7
- ↑ Peter Atkins; Julio de Paula. Physical Chemistry (8ª ed. W.H.Freeman 2006) p. 756 ISBN 0-7167-8759-8
- ↑ Drago, R.S. Physical Methods in Chemistry (W.B.Saunders 1977) p. 563 ISBN 0-7216-3184-3
- ↑ Brey Abalo, José Javier;de la Rubia Pacheco, Juan;de la Rubia Sanchez, Javier; Mecánica Estadística Madrid, (Universidad Nacional de Educación a Distancia, 2008) p. 109 ISBN 978-84-362-4572-1