Ecuación de Sellmeier

En óptica, la ecuación de Sellmeier es una relación empírica entre el índice de refracción n y la longitud de onda λ para un medio transparente particular. La forma habitual de la ecuación para cristales es:

Índice de refracción vs. longitud de onda para vidrio BK7, mostrando la ecuación Sellmeier (línea roja)

Igual que el gráfico anterior, pero con la ecuación de Cauchy (línea azul) para comparar. Mientras que la ecuación de Cauchy se desvía significativamente de los índices de refracción medidos fuera de la región visible (que está sombreada en rojo), la ecuación de Sellmeier (línea verde discontinua) no.

$n^{2}(\lambda )=1+{\frac {B_{1}\lambda ^{2}}{\lambda ^{2}-C_{1}}}+{\frac {B_{2}\lambda ^{2}}{\lambda ^{2}-C_{2}}}+{\frac {B_{3}\lambda ^{2}}{\lambda ^{2}-C_{3}}},$

donde B_1,2,3 y C_1,2,3 son los coeficientes de Sellmeier determinados experimentalmente. Habitualmente, estos coeficientes suelen calcularse para λ en micrómetros. Hay que darse cuenta de que esta λ es la longitud de onda en el vacío, no en el material en el que medimos, donde es λ/n(λ).

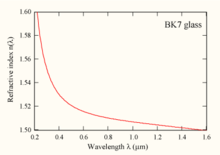
Esta ecuación se utiliza para determinar la dispersión de la luz en un medio refractivo. Una forma diferente de la ecuación se usa a veces para ciertos tipos de materiales como, por ejemplo, cristales.

La ecuación fue deducida en 1871 por Wilhelm Sellmeier, a partir del desarrollo del trabajo de Augustin Cauchy en la ecuación de Cauchy para modelos de dispersión.

Coeficientes

Tabla de coeficientes para la ecuación de Sellmeier[1]
Material	B1	B2	B3	C1	C2	C3
Vidrio borosilicatado	1.03961212	0.231792344	1.01046945	6.00069867×10−3µm²	2.00179144×10−2µm²	1.03560653×102µm²
Zafiro (para el rayo ordinario)	1.43134930	0.65054713	5.3414021	5.2799261×10−3µm²	1.42382647×10−2µm²	3.25017834×102µm²
Zafiro (para el rayo extraordinario)	1.5039759	0.55069141	6.5927379	5.48041129×10−3µm²	1.47994281×10−2µm²	4.0289514×102µm²
Sílice fundida	0.696166300	0.407942600	0.897479400	4.67914826×10−3µm²	1.35120631×10−2µm²	97.9340025 µm²
Fluoruro de magnesio	0.48755108	0.39875031	2.3120353	0.001882178	0.008951888	566.13559 µm²

Véase también

• Relaciones de Kramers-Kronig

Enlaces externos

• Archivo PDF que da los coeficientes de Sellmeier para diferentes tipos de vidrios y materiales ópticos comunes.
• Archivo XLS con coeficientes de dispersión y otras propiedades ópticas de los vidrios Schott.
• Página web donde se puede calcular el índice de refracción a partir de los coeficientes de Sellmeier.
• Annalen der Physik - libro de acceso libre.

• Datos: Q1428292