Dodecaedro excavado
En geometría, el dodecaedro excavado es un poliedro estrellado que se parece a un dodecaedro con pirámides cóncavas en lugar de sus caras. Su superficie exterior representa la estelación Ef1g1 del icosaedro. Aparece en el libro Polyhedron Models de Magnus Wenninger como modelo 28, catalogado como la tercera estelación del icosaedro.
| Dodecaedro excavado | ||
|---|---|---|
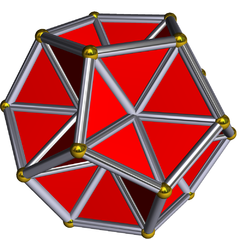 Dodecaedro excavado | ||
| Tipo | Poliedro estrellado (W28, 26/59) | |
| Caras | 60 (triángulos equiláteros) // 20 (hexagramas) | |
| Polígonos que forman las caras | Triángulos equiláteros // Hexágonos estrellados | |
| Aristas | 90 | |
| Vértices | 32 | |
| Configuración de vértices |
 Hexágono cóncavo | |
| Poliedro dual | Autodual | |
| Propiedades | ||
|
Característica de Euler: F = 20, E = 60 V = 20 (χ = −20) Diagrama:  Poliedro noble, isogonal, autodual | ||
Descripción
editarLos 20 vértices y 30 de sus 60 aristas pertenecen a su contorno dodecaédrico. Las otras 30 aristas internas son más largas y forman parte de un gran dodecaedro estrellado (cada una coincide con uno de los 30 bordes del núcleo icosaédrico). Posee 20 caras, correspondientes a sus 20 vértices. Cada cara es un hexágono autointersecante con bordes largos y cortos alternos y ángulos de 60°. Los triángulos equiláteros que tocan un borde corto son parte de la cara. Cada grupo de tres lados cortos de las caras hexagrámicas situadas entre los lados largos forman una cara del núcleo icosaédrico.
| Núcleo | Bordes largos | Caras | Envolvente | Corte |
|---|---|---|---|---|
| Icosaedro |
Gran dodecaedro estrellado |
Dodecaedro |
Cara hexagonal (en azul) |
Facetado del dodecaedro
editarEl dodecaedro excavado tiene la misma forma externa que un facetado del dodecaedro formado por 20 hexágonos autointersecantes como caras. Los hexágonos no convexos que forman las caras se pueden dividir en cuatro triángulos equiláteros cada uno, tres de los cuales son del mismo tamaño. Un verdadero dodecaedro excavado tiene los tres triángulos equiláteros congruentes como caras verdaderas del poliedro, mientras que el triángulo equilátero interior no está presente.
Los 20 vértices de la envolvente convexa coinciden con la disposición de vértices del dodecaedro.
-
Una de las caras del hexágono estrellado resaltada
-
Cara como una faceta del dodecaedro
-
Teselado uniforme 66-t2
El volumen facetado es un poliedro noble. Con seis caras de seis lados alrededor de cada vértice, es topológicamente equivalente a un espacio cociente del teselado hexagonal de orden 6 hiperbólico {6,6}, y es del tipo abstracto {6,6}6. Es uno de los diez poliedros regulares abstractos de índice dos con sus vértices en una órbita.[1][2]
Fórmulas
editar| Dimensiones de un dodecaedro excavado de arista a | ||
|---|---|---|
| Volumen | ||
| Superficie | ||
| Altura de las pirámides | ||
| Arista del icosaedro interior | ||
| Ángulo diedro 1: ≈ 138° 11′ 23″ |
||
| Ángulo diedro 2: ≈ 41° 48′ 37″ |
||
Poliedros relacionados
editar|
Un pentaquis dodecaedro (izda) y el poliedro excavado con pirámides invertidas (derecha) tienen la misma superficie |
Las caras del dodecedro excavado (izquierda) son parte de las caras del gran icosaedro (derecha). Para verlo, basta con extender los bordes cortos de un hexágono hasta que se encuentren con el triángulo que lo contiene. Reemplazando cada hexágono auto intersecante por uno convexo se obtiene una figura que contiene los bordes del compuesto de cinco cubos (centro). Pero esto no es realmente un poliedro, porque cada uno de estos bordes pertenece únicamente a una sola cara |
|
El gran dodecaedro (izquierda) es un icosaedro excavado. También tiene 60 triángulos visibles. Pero a diferencia del dodecaedro excavado (derecha) tiene caras convexas y, por lo tanto, no tiene bordes internos |
Referencias
editar- ↑ Regular Polyhedra of Index Two, I Anthony M. Cutler, Egon Schulte, 2010
- ↑ Regular Polyhedra of Index Two, II Beitrage zur Algebra und Geometrie 52(2):357-387 · November 2010, Table 3, p.27
Bibliografía
editar- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 6.2 Stellating the Platonic solids, pp.96-104