Distribución gamma

En teoría de probabilidad y Estadística, la distribución gamma es una distribución con dos parámetros que pertenece a las distribuciones de probabilidad continuas. La distribución exponencial, distribución de Erlang y la distribución χ² son casos particulares de la distribución gamma. Hay dos diferentes parametrizaciones que suelen usarse

1. Con parámetro de forma $k$ y parámetro de escala $\theta$.
2. Con parámetro de forma $\alpha =k$ y parámetro inverso de escala $\lambda =1/\theta$.

Gamma
Parámetros	$\alpha >0$ forma (real) $\lambda >0$ escala (real)
Dominio	$x\in (0,\infty )$
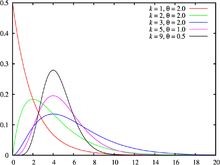
Función de densidad (pdf)	${\frac {\lambda (\lambda x)^{\alpha -1}e^{-\lambda x}}{\Gamma (\alpha )}}$
Función de distribución (cdf)	${\frac {1}{\Gamma (\alpha )}}\;\gamma (\alpha ,\lambda x)$
Media	${\frac {\alpha }{\lambda }}$
Moda	${\frac {\alpha -1}{\lambda }}{\text{ por }}\alpha \geq 1$, $0{\text{ por }}\alpha <1$
Varianza	${\frac {\alpha }{\lambda ^{2}}}$
Entropía	$\alpha -\ln \lambda +\ln \Gamma (\alpha )+(1-\alpha )\psi (\alpha )$
Función generadora de momentos (mgf)	$\left({\frac {\lambda }{\lambda -t}}\right)^{\alpha }\quad t<\lambda$
Función característica	$\left({\frac {\lambda }{\lambda -it}}\right)^{\alpha }$

Función de Densidad de una Gama.

Definición

Notación

Si una variable aleatoria continua $X$ tiene distribución gamma con parámetros $\alpha >0$ y $\lambda >0$ entonces escribiremos $X\sim \Gamma (\alpha ,\lambda )$.

Función de Densidad

Si $X\sim \Gamma (\alpha ,\lambda )$ entonces su función de densidad es

$f_{X}(x)={\frac {\lambda }{\Gamma (\alpha )}}(\lambda x)^{\alpha -1}e^{-\lambda x}$

para $x>0$ donde

$\Gamma (\alpha )=\int _{0}^{\infty }t^{\alpha -1}e^{-t}dt$

es la función gamma y satisface

1. $\Gamma (2)=\Gamma (1)=1$
2. Para cualquier $\alpha >0$ se cumple que $\Gamma (\alpha +1)=\alpha \Gamma (\alpha )$
3. Si $n\in \mathbb {Z} ^{+}$ entonces $\Gamma (n+1)=n!$
4. $\Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}$
5. Si $n\in \mathbb {Z} ^{+}$ entonces $\Gamma \left({\frac {n}{2}}\right)={\frac {{\sqrt {\pi }}(n-1)!}{2^{n-1}\left({\frac {n-1}{2}}\right)!}}$

Función de Densidad Acumulada

La función de distribución acumulada de una variable aleatoria $X\sim \Gamma (\alpha ,\lambda )$ está dada por

$F_{X}(x)=\int _{0}^{x}{\frac {\lambda }{\Gamma (\alpha )}}(\lambda y)^{\alpha -1}e^{-\lambda y}\;dy$

Si $X$ es una variable aleatoria tal que $X\sim \Gamma (n,\lambda )$ donde $n\in \mathbb {Z} ^{+}$ (es decir, $X$ tiene una distribución de Erlang) entonces su función de distribución acumulada está dada por

${\begin{aligned}F_{X}(x)&=1-\sum _{k=0}^{n-1}{\frac {(\lambda x)^{k}}{k!}}e^{-\lambda x}\\&=\sum _{k=n}^{\infty }{\frac {(\lambda x)^{k}}{k!}}e^{-\lambda x}\end{aligned}}$

Propiedades

Si $X$ es una variable aleatoria tal que $X\sim \Gamma (\alpha ,\lambda )$ entonces $X$ satisface algunas propiedades.

Media

La media de la variable aleatoria $X$ es:

${\text{E}}[X]=\alpha /\lambda$

Varianza

La varianza de la variable aleatoria $X$ es

${\text{Var}}[X]={\frac {\alpha }{\lambda ^{2}}}$

Momentos

El $n$-ésimo momento de la variable aleatoria $X$ es

$\operatorname {E} [X^{n}]={\frac {\alpha (\alpha +1)\cdots (\alpha +n-1)}{\lambda ^{n}}}$

para $n\in \mathbb {N}$.

Función generadora de momentos

La función generadora de momentos está dada por

$M_{X}(t)=\left({\frac {\lambda }{\lambda -t}}\right)^{\alpha }$

para $\lambda >t$.

Suma de Gammas

Si $X_{i}\sim \Gamma (\alpha _{i},\lambda )$ para $i=1,2,\dots ,n$ son variables aleatorias independientes entonces

$\sum _{i=1}^{n}X_{i}\sim \Gamma \left(\sum _{i=1}^{n}\alpha _{i},\lambda \right)$

Escalar

Si $X\sim \Gamma (\alpha ,\lambda )$ entonces para cualquier $c>0$

$cX\sim \Gamma \left(\alpha ,\lambda /c\right)$

Media Logarítmica

Puede demostrarse que

$\operatorname {E} [\ln(X)]=\psi (\alpha )-\ln(\lambda )$

donde $\psi$ es la función digamma.

Cálculo de Probabilidades en R

Se puede utilizar R (lenguaje de programación) para hallar los valores de la función de densidad $f(x)$ y la función de distribución $F(x)$ de una variable aleatoria continua $X\sim \Gamma (\alpha ,\lambda )$.

Función de densidad

Para $x>0$, la función de densidad de la distribución Gamma está dada por

$f_{X}(x)={\frac {\lambda }{\Gamma (\alpha )}}(\lambda x)^{\alpha -1}e^{-\lambda x}$

entonces para evaluar la función de densidad $f_{X}(x)$ utilizamos el siguiente código

# d=density function
dgamma(x,α,λ)

Función de Distribución

La función de distribución acumulada de la distribución Gamma está dada por

$F_{X}(x)=\int _{0}^{x}{\frac {\lambda }{\Gamma (\alpha )}}(\lambda y)^{\alpha -1}e^{-\lambda y}\;dy$

para $x>0$, se puede utilizar el siguiente código para evaluar al función de distribución acumulada $F_{X}(x)$

# p=probability distribution function
pgamma(x,α,λ)

Distribuciones Relacionadas

• Si $X_{1},X_{2},\dots ,X_{n}$ son variables aleatorias independientes e idénticamente distribuidas tales que $X_{i}\sim {\text{Exp}}(\lambda )$ entonces $\sum \limits _{i=1}^{n}X_{i}\sim \Gamma \left(n,\lambda \right)$, a esta distribución se le conoce como distribución de Erlang y es un caso particular de la distribución gama cuando el parámetro $\alpha =n\in \mathbb {N}$.

• Si $X\sim \Gamma \left(1,\lambda \right)$ entonces $X\sim {\text{Exp}}(\lambda )$.
• Si $X\sim \Gamma \left({\frac {n}{2}},{\frac {1}{2}}\right)$ con $n\in \mathbb {N}$ entonces $X\sim \chi _{n}^{2}$.

Véase también

• Distribución Exponencial
• Distribución Beta
• Distribución de Erlang
• Distribución χ²

Enlaces externos

• Weisstein, Eric W. «GammaDistribution». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• [1] Archivado el 13 de abril de 2020 en Wayback Machine. Calcular la probabilidad de una distribución Gamma con R (lenguaje de programación)

• Datos: Q117806
• Multimedia: Gamma distribution / Q117806