Corriente geostrófica
Una corriente geostrófica es una corriente oceánica en la que la fuerza del gradiente de presión se equilibra con el efecto Coriolis. La dirección del flujo geostrófico es paralela a las isobaras, con la alta presión a la derecha del flujo en el hemisferio norte y la alta presión a la izquierda en el hemisferio sur. Este concepto es familiar de los mapas meteorológicos, cuyas isobaras muestran la dirección del flujo geostrófico en la atmósfera.

El flujo geostrófico puede ser barotrópico o baroclínico. Una corriente geostrófica también se puede considerar como una onda de aguas someras en rotación con una frecuencia de cero. El principio de geostrofia es útil para los oceanógrafos porque les permite inferir corrientes oceánicas a partir de mediciones de la altura de la superficie del mar (mediante la combinación de altimetría satelital y gravimetría) o de perfiles verticales de la densidad del agua de mar tomada por barcos o boyas autónomas. Las principales corrientes de los océanos del mundo, como la corriente del Golfo, la corriente de Kuroshio, la corriente de Agulhas y la corriente Circumpolar Antártica, están aproximadamente en equilibrio geostrófico y son ejemplos de corrientes geostróficas.
Explicación sencilla
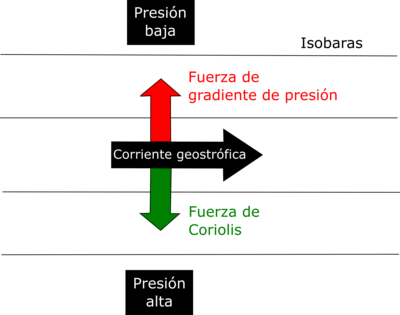
editarEl agua de mar tiende naturalmente a moverse de una región de alta presión (o nivel del mar alto) a una región de baja presión (o nivel del mar bajo). La fuerza que empuja el agua hacia la región de baja presión se llama fuerza de gradiente de presión. En un flujo geostrófico, en lugar de que el agua se mueva de una región de alta presión (o nivel del mar alto) a una región de baja presión (o nivel del mar bajo), se mueve a lo largo de las líneas de presión igual (isobaras). Esto ocurre porque la Tierra está girando.
La rotación de la tierra da como resultado una "fuerza" que se siente cuando el agua se mueve de lo alto a lo bajo, conocida como fuerza de Coriolis. La fuerza de Coriolis actúa en ángulos rectos al flujo, y cuando equilibra la fuerza del gradiente de presión, el flujo resultante se conoce como geostrófico.
Como se indicó anteriormente, la dirección del flujo es con la alta presión a la derecha del flujo en el hemisferio norte y la alta presión a la izquierda en el hemisferio sur. La dirección del flujo depende del hemisferio, porque la dirección de la fuerza de Coriolis es opuesta en los diferentes hemisferios.
Formulación
editarLas ecuaciones geostróficas son una forma simplificada de las ecuaciones de Navier-Stokes en un marco de referencia giratorio. En particular, se supone que no hay aceleración (estado estable), que no hay viscosidad y que la presión es hidrostática. El saldo resultante es (Gill, 1982):
Dónde Es el Parámetro de coriolis , es la densidad, es la presión y son las velocidades en las direcciones respectivamente.
Una propiedad especial de las ecuaciones geostróficas es que satisfacen la versión de estado estable de la ecuación de continuidad. Es decir:
Ondas giratorias de frecuencia cero.
editarLas ecuaciones que gobiernan una onda de agua superficial lineal y rotatoria son:
El supuesto de estado estable hecho anteriormente (sin aceleración) es:
Alternativamente, podemos asumir una dependencia en el tiempo, periódica, de tipo onda:
En este caso, si configuramos Hemos revertido a las ecuaciones geostróficas anteriores. Por lo tanto, una corriente geostrófica se puede considerar como una onda de agua superficial en rotación con una frecuencia de cero.
Véase también
editarReferencias
editar- Gill, Adrian E. (1982), Atmosphere-Ocean Dynamics, International Geophysics Series 30, Oxford: Academic Press, ISBN 0-12-283522-0.