Coordenadas esferoidales prolatas

Las coordenadas esferoidales prolatas (también denominadas alargadas) son un sistema de referencia tridimensional ortogonal que resulta de rotar un sistema de coordenadas elípticas bidimensional alrededor del eje focal de la elipse, es decir, respecto el eje de simetría en el que se encuentran los focos. La rotación alrededor del otro eje produce un sistema de coordenadas esferoidales oblatas. Las coordenadas esferoidales prolatas también pueden considerarse como un caso límite de coordenadas elipsoidales en las que los dos ejes principales más pequeños tienen la misma longitud.

Las tres superficies coordenadas del sistema de coordenadas esferoidales prolatas. El esferoide alargado rojo (esfera estirada) corresponde a μ = 1, y el hiperboloide de dos hojas azul corresponde a ν = 45°. El semiplano amarillo corresponde a φ = −60°, que se mide en relación con el eje x (resaltado en verde). La esfera negra representa el punto de intersección de las tres superficies, que tiene unas coordenadas cartesianas de aproximadamente (0.831, −1.439, 2.182)

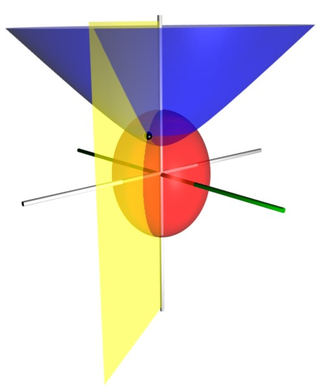
Las coordenadas esferoidales prolatas pueden usarse para resolver ecuaciones en derivadas parciales en los que las condiciones de contorno coinciden con su simetría y forma, como resolver un campo producido por dos centros, que se toman como los focos en el eje z. Un ejemplo es resolver la función de onda de un electrón que se mueve en el campo electromagnético de dos núcleos con carga positiva, como en el catión dihidrógeno, H₂⁺. Otro ejemplo es modelizar el campo eléctrico generado por dos puntas pequeñas de electrodo. Otros casos límite incluyen áreas generadas por un segmento de línea (µ = 0) o una línea con un segmento faltante (ν=0). La estructura electrónica de moléculas diatómicas generales con muchos electrones también se puede resolver con excelente precisión en el sistema de coordenadas esferoidales prolatas.​

Definición

Coordenadas esferoidales prolatas μ and ν para a = 1. Las líneas de valores iguales de μ y μ se muestran en el plano xz, es decir, para φ = 0. Las superficies de valores constantes μ y ν se obtienen por rotación alrededor del eje z, de modo que el diagrama es válido para cualquier plano que contenga el eje z: es decir, para cualquier φ

La definición más común de las coordenadas esferoidales prolatas $(\mu ,\nu ,\varphi )$ es

$x=a\sinh \mu \sin \nu \cos \varphi$

$y=a\sinh \mu \sin \nu \sin \varphi$

$z=a\cosh \mu \cos \nu$

donde $\mu$ es un número real no negativo y $\nu \in [0,\pi ]$. El ángulo azimutal $\varphi$ pertenece al intervalo $[0,2\pi ]$.

La identidad trigonométrica

${\frac {z^{2}}{a^{2}\cosh ^{2}\mu }}+{\frac {x^{2}+y^{2}}{a^{2}\sinh ^{2}\mu }}=\cos ^{2}\nu +\sin ^{2}\nu =1$

muestra que las superficies de $\mu$ constante forman esferoides prolatos, ya que son elipses rotadas sobre el eje que une sus focos. De manera similar, la identidad trigonométrica hiperbólica

${\frac {z^{2}}{a^{2}\cos ^{2}\nu }}-{\frac {x^{2}+y^{2}}{a^{2}\sin ^{2}\nu }}=\cosh ^{2}\mu -\sinh ^{2}\mu =1$

muestra que las superficies de $\nu$ constante forman hiperboloides de revolución.

Las distancias desde los focos ubicados en $(x,y,z)=(0,0,\pm a)$ son

$r_{\pm }={\sqrt {x^{2}+y^{2}+(z\mp a)^{2}}}=a(\cosh \mu \mp \cos \nu ).$

Factores de escala

Los factores de escala para las coordenadas elípticas $(\mu ,\nu )$ son iguales

$h_{\mu }=h_{\nu }=a{\sqrt {\sinh ^{2}\mu +\sin ^{2}\nu }}$

mientras que el factor de escala azimutal es

$h_{\varphi }=a\sinh \mu \sin \nu ,$

lo que da como resultado la métrica

${\begin{aligned}ds^{2}&=h_{\mu }^{2}d\mu ^{2}+h_{\nu }^{2}d\nu ^{2}+h_{\varphi }^{2}d\varphi ^{2}\\&=a^{2}\left[(\sinh ^{2}\mu +\sin ^{2}\nu )d\mu ^{2}+(\sinh ^{2}\mu +\sin ^{2}\nu )d\nu ^{2}+(\sinh ^{2}\mu \sin ^{2}\nu )d\varphi ^{2}\right].\end{aligned}}$

En consecuencia, un elemento de volumen infinitesimal es igual a

$dV=a^{3}\sinh \mu \sin \nu (\sinh ^{2}\mu +\sin ^{2}\nu )\,d\mu \,d\nu \,d\varphi$

y el laplaciano puede escribirse como

${\begin{aligned}\nabla ^{2}\Phi ={}&{\frac {1}{a^{2}(\sinh ^{2}\mu +\sin ^{2}\nu )}}\left[{\frac {\partial ^{2}\Phi }{\partial \mu ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \nu ^{2}}}+\coth \mu {\frac {\partial \Phi }{\partial \mu }}+\cot \nu {\frac {\partial \Phi }{\partial \nu }}\right]\\[6pt]&{}+{\frac {1}{a^{2}\sinh ^{2}\mu \sin ^{2}\nu }}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}\end{aligned}}$

Otros operadores diferenciales como $\nabla \cdot \mathbf {F}$ y $\nabla \times \mathbf {F}$ pueden expresarse en las coordenadas $(\mu ,\nu ,\varphi )$ sustituyendo los factores de escala en las fórmulas generales que se encuentran en el artículo dedicado a las coordenadas ortogonales.

Definición alternativa

En principio, una definición de coordenadas esferoidales prolatas podría ser degenerada. En otras palabras, un único conjunto de coordenadas podría corresponder a dos puntos en coordenadas cartesianas. Esto se ilustra aquí con dos esferas negras, una en cada hoja del hiperboloide y ubicadas en (x, y, ±z). Sin embargo, ninguna de las definiciones presentadas aquí es degenerada

A veces se utiliza un conjunto alternativo y geométricamente intuitivo de coordenadas esferoidales prolatas $(\sigma ,\tau ,\varphi )$, donde $\sigma =\cosh \mu$ y $\tau =\cos \nu$. Por lo tanto, las superficies de $\sigma$ constante son esferoides alargados, mientras que las superficies de $\tau$ constante son hiperboloides de revolución. La coordenada $\tau$ pertenece al intervalo [-1, 1], mientras que la coordenada $\sigma$ debe ser mayor o igual a uno.

Las coordenadas $\sigma$ y $\tau$ tienen una relación simple con las distancias a los focos $F_{1}$ y $F_{2}$. Para cualquier punto en el plano, la suma $d_{1}+d_{2}$ de sus distancias a los focos es igual a $2a\sigma$, mientras que su diferencia $d_{1}-d_{2}$ es igual a $2a\tau$. Por lo tanto, la distancia a $F_{1}$ es $a(\sigma +\tau )$, mientras que la distancia a $F_{2}$ es $a(\sigma -\tau )$ (debe recordarse que $F_{1}$ y $F_{2}$ se encuentran en $z=-a$ y $z=+a$, respectivamente). Esto da las siguientes expresiones para $\sigma$, $\tau$ y $\varphi$:

$\sigma ={\frac {1}{2a}}\left({\sqrt {x^{2}+y^{2}+(z+a)^{2}}}+{\sqrt {x^{2}+y^{2}+(z-a)^{2}}}\right)$

$\tau ={\frac {1}{2a}}\left({\sqrt {x^{2}+y^{2}+(z+a)^{2}}}-{\sqrt {x^{2}+y^{2}+(z-a)^{2}}}\right)$

$\varphi =\arctan \left({\frac {y}{x}}\right)$

A diferencia de las análogas coordenadas esferoidales oblatas, las coordenadas del esferoide prolato (σ, τ, φ) no están degeneradas. En otras palabras, existe una correspondencia única y reversible entre ellas y las coordenadas cartesianas

$x=a{\sqrt {(\sigma ^{2}-1)(1-\tau ^{2})}}\cos \varphi$

$y=a{\sqrt {(\sigma ^{2}-1)(1-\tau ^{2})}}\sin \varphi$

$z=a\ \sigma \ \tau$

Factores de escala alternativos

Los factores de escala para las coordenadas elípticas alternativas $(\sigma ,\tau ,\varphi )$ son

$h_{\sigma }=a{\sqrt {\frac {\sigma ^{2}-\tau ^{2}}{\sigma ^{2}-1}}}$

$h_{\tau }=a{\sqrt {\frac {\sigma ^{2}-\tau ^{2}}{1-\tau ^{2}}}}$

mientras que el factor de escala azimutal es

$h_{\varphi }=a{\sqrt {\left(\sigma ^{2}-1\right)\left(1-\tau ^{2}\right)}}$

Por lo tanto, el elemento de volumen infinitesimal se convierte en

$dV=a^{3}(\sigma ^{2}-\tau ^{2})\,d\sigma \,d\tau \,d\varphi$

y el laplaciano es igual a

${\begin{aligned}\nabla ^{2}\Phi ={}&{\frac {1}{a^{2}(\sigma ^{2}-\tau ^{2})}}\left\{{\frac {\partial }{\partial \sigma }}\left[\left(\sigma ^{2}-1\right){\frac {\partial \Phi }{\partial \sigma }}\right]+{\frac {\partial }{\partial \tau }}\left[(1-\tau ^{2}){\frac {\partial \Phi }{\partial \tau }}\right]\right\}\\&{}+{\frac {1}{a^{2}(\sigma ^{2}-1)(1-\tau ^{2})}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}\end{aligned}}$

Otros operadores diferenciales como $\nabla \cdot \mathbf {F}$ y $\nabla \times \mathbf {F}$ se pueden expresar en las coordenadas $(\sigma ,\tau )$ sustituyendo los factores de escala en las fórmulas generales que se encuentran en el artículo dedicado a las coordenadas ortogonales.

Como es el caso con coordenadas esféricas, la ecuación de Laplace se puede resolver por el método de separación de variables para obtener soluciones en la forma armónicos esferoidales prolatos, cuyo uso es conveniente cuando las condiciones de contorno se definen en una superficie con una coordenada esferoidal prolata constante (véase Smythe, 1968).

Bibliografía

Sin convención de ángulos

• Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 661.  Utiliza ?₁ = a cosh µ, ?₂ = sen ?, y ?₃ = cos f.
• Zwillinger D (1992). Handbook of Integration. Boston, MA: Jones and Bartlett. p. 114. ISBN 0-86720-293-9.  Igual que Morse y Feshbach (1953), sustituyendo ?_k por u_k.
• Smythe, WR (1968). Static and Dynamic Electricity (3rd edición). New York: McGraw-Hill. 
• Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. p. 97. LCCN 67025285.  Utiliza las coordenadas ? = cosh µ, ? = sen ?, y f.

Con convención de ángulos

• Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 177. LCCN 59014456.  Korn y Korn utilizan las coordenadas (µ, ?, f), pero también introducen las coordenadas degeneradas (s, t, f).
• Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 180—182. LCCN 55010911.  Similar a Korn y Korn (1961), pero utiliza colatitud ? = 90° - ? en lugar de latitud ?.
• Moon PH, Spencer DE (1988). «Prolate Spheroidal Coordinates (η, θ, ψ)». Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print edición). New York: Springer Verlag. pp. 28—30 (Table 1.06). ISBN 0-387-02732-7.  Moon y Spencer utilizan la convención de colatitud ? = 90° - ?, y renombran f como ?.

Con convención de ángulos inusual

• Landau LD, Lifshitz EM, Pitaevskii LP (1984). Electrodynamics of Continuous Media (Volume 8 of the Course of Theoretical Physics) (2nd edición). New York: Pergamon Press. pp. 19—29. ISBN 978-0-7506-2634-7.  Trata las coordenadas esferoidales prolatas como un caso límite de la ellipsoidal coordinates general. Utiliza coordenadas (?, ?, ?) que tienen las unidades de distancia al cuadrado.

Enlaces externos

• Descripción de MathWorld de las coordenadas esferoidales prolatas

• Datos: Q7249552