Archivo:Thiel-Sen estimator.svg
Tamaño de esta previsualización PNG del archivo SVG: 572 × 599 píxeles. Otras resoluciones: 229 × 240 píxeles · 458 × 480 píxeles · 733 × 768 píxeles · 978 × 1024 píxeles · 1955 × 2048 píxeles · 2936 × 3075 píxeles.
Ver la imagen en su resolución original ((Imagen SVG, nominalmente 2936 × 3075 pixels, tamaño de archivo: 37 kB))
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 18:59 3 nov 2011 |  | 2936 × 3075 (37 kB) | David Eppstein | Darker green, thicker lines |
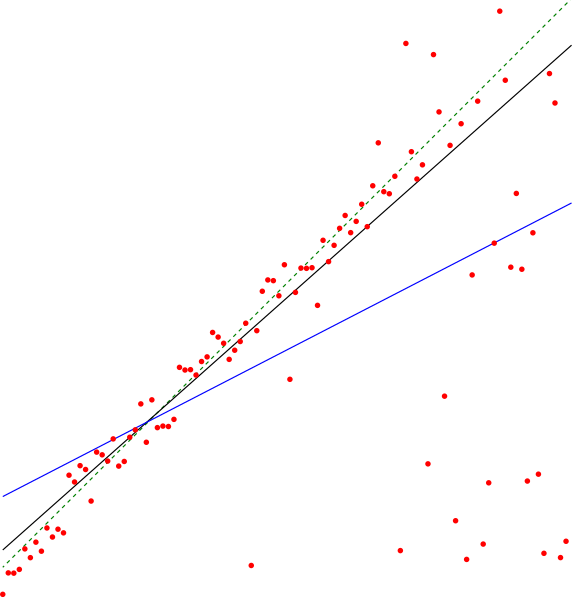
| 23:40 3 jul 2011 |  | 2936 × 3075 (37 kB) | David Eppstein | {{Information |Description ={{en|1=The en:Theil–Sen estimator (black line) of a set of sample points, compared to the simple linear regression line (blue). The points were generated by adding a small amount of jitter to points on the green dashe |
Usos del archivo
La siguiente página usa este archivo:
Uso global del archivo
Las wikis siguientes utilizan este archivo:
- Uso en ar.wikipedia.org
- Uso en el.wiktionary.org
- Uso en en.wikipedia.org
- Uso en fa.wikipedia.org
- Uso en hy.wikipedia.org
- Uso en ko.wikipedia.org
- Uso en ru.wikipedia.org
- Uso en zh.wikipedia.org